题目内容
如图，抛物线y= -x2+2x+m（m＜0）与x轴相交于点A（x1，0）、B（x2，0），点A在点B的左侧．当x=x2-2时，y____0（填“＞”“=”或“＜”号）．
＜
【解析】试题分析：根据题意可得函数的对称轴为x=1，∵0＜＜1，则1＜＜2，∴x=－2＜0，根据图象可得：当x＜0时，y＜0.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
正方形既是_________图形，又是_____________图形
轴对称 中心对称
【解析】正方形既是轴对称图形又是中心对称图形.
故答案：轴对称，中心对称. 在平面直角坐标系中，点A的坐标是（2，3），点B的坐标是（2，-2），若把线段AB向左平移3个单位后变为A′B′，则A′B′可表示为 ．
x=-1（-2≤y≤3）．
【解析】
试题解析：∵点A的坐标是（2，3），点B的坐标是（2，-2），若把线段AB向左平移3个单位后变为A′B′，
∴点A′的坐标为（-1，3）；点B′的坐标为（-1，-2），
∴线段A′B′可表示为 x=-1（-2≤y≤3）． 将点P向左平移2个单位，再向上平移1个单位，得到P′(－1,3)，则点P的坐标是_____.
(1,2)
【解析】试题分析：根据平移特征即可判断结果。
将点P向左平移2个单位，再向上平移1个单位得到P′(-1，3)，则点P的坐标是(1，2) . 已知抛物线y= -x2+mx+（7-2m）（m为常数）．
（1）证明：不论m为何值，抛物线与x轴恒有两个不同的交点；
（2）若抛物线与x轴的交点A（x1，0）、B（x2，0）的距离为AB=4（A在B的左边），且抛物线交y轴的正半轴于C，求抛物线的解析式．
（1）证明见解析；（2）抛物线的解析式为y= -x2+2x+3．
【解析】试题分析：（1）要证明抛物线与x轴恒有两个不同的交点证明抛物线的判别式是正数，所以证明判别式是正数即可解决问题；
（2）首先由AB=4可以得|x2-x1|=4，而（x2-x1）2=（x2-x1）2-4x1x2=16，然后利用根与系数的关系即可得到关于m方程，解方程即可求出m，也就求出了抛物线的解析式．
试题... 已知函数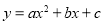
的图象如图所示，那么关于x的方程
的根的情况是（ ）
A．无实数根
B．有两个相等实数根
C．有两个异号实数
D．有两个同号不等实数根
D．
【解析】
试题分析：∵的图象与x轴有两个交点，顶点坐标的纵坐标是﹣3，∵方程，∴时，即是y=﹣2求x的值，由图象可知：有两个同号不等实数根．故选D． 已知二次函数y=x2+bx-2的图象与x轴的一个交点为（1，0），则它与x轴的另一个交点坐标是（ ）
A. （1，0） B. （2，0） C. （-2，0） D. （-1，0）
C
【解析】试题分析：把x＝1，y＝0代入y＝x2＋bx－2得：
0＝1＋b－2，
∴b＝1，
∴对称轴为x＝＝，
∴x＝＝，
∴x2＝－2，
它与x轴的另一个交点坐标是（－2，0）．
故选C． 下面的多项式中，能因式分解的是（ ）
A. m2+n B. m2﹣m+1 C. m2﹣n D. m2﹣2m+1
D
【解析】A. m2+n不能因式分解；
B. m2﹣m+1不能因式分解；
C. m2﹣n不能因式分解；
D. m2﹣2m+1=(m-1)2,能因式分解.
故选D.