题目内容
已知函数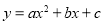
的图象如图所示，那么关于x的方程
的根的情况是（ ）
A．无实数根
B．有两个相等实数根
C．有两个异号实数
D．有两个同号不等实数根
D．
【解析】
试题分析：∵的图象与x轴有两个交点，顶点坐标的纵坐标是﹣3，∵方程，∴时，即是y=﹣2求x的值，由图象可知：有两个同号不等实数根．故选D．
下列说法中正确的是（ ）
A. 能重合的图形一定是成轴对称图形
B. 成中心对称的图形一定是重合的图形
C. 两个成中心对称的图形的对称点连线不一定过对称中心
D. 两个会重合的三角形一定关于某一点成中心对称
B
【解析】试题解析：轴对称图形是沿对称轴折叠重合的图形，而全等的图形即可重合，所以A错误；
中心对称的图形全等即可重合，所以B正确；
成中心对称的图形的对称点连线一定过对称中心，所以C错误；
全等的三角形关于某一点旋转180°后可以重合，才是成中心对称的．所以D错误.
故选B. 在平面直角坐标系中，将图形沿x轴正方向平移3个单位，变化前后对应点 纵坐标不变， 横坐标增加3个单位．
纵；横
【解析】
试题分析：图形沿x轴正方向平移，改变的是y值，x值不变。 如图，A，B的坐标为（2，0），（0，1），若将线段AB平移至A1B1，则a+b的值为（ ）
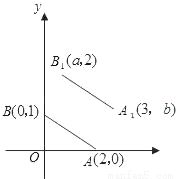
A. 2 B. 3 C. 4 D. 5
A
【解析】由B点平移前后的纵坐标分别为1,2,可得B点向上平移了1个单位,由A点平移前后的横坐标分别是为2,3,可得A点向右平移了1个单位,由此得线段AB的平移的过程是:向上平移1个单位,再向右平移1个单位,所以点A,B均按此规律平移,由此可得a=0+1=1,b=0+1=1,故a+b=2,故选:A. 如图，抛物线y= -x2+2x+m（m＜0）与x轴相交于点A（x1，0）、B（x2，0），点A在点B的左侧．当x=x2-2时，y____0（填“＞”“=”或“＜”号）．
＜
【解析】试题分析：根据题意可得函数的对称轴为x=1，∵0＜＜1，则1＜＜2，∴x=－2＜0，根据图象可得：当x＜0时，y＜0. 如图，将二次函数y=31x2-999x+892的图形画在坐标平面上，判断方程31x2-999x+892=0的两根，下列叙述何者正确（ ）
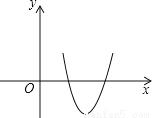
A. 两根相异，且均为正根
B. 两根相异，且只有一个正根
C. 两根相同，且为正根
D. 两根相同，且为负根
A
【解析】∵二次函数y=31x2-999x+892的图象与x轴有两个交点，且与x轴的正半轴相交，
∴方程31x2-999x+892=0有两个正实根．
故选：A． 二次函数y= -x2+2x+k的部分图象如图所示，则关于x的一元二次方程-x2+2x+k=0的一个解x1=3，另一个解x2=（ ）
A. 1 B. -1 C. -2 D. 0
B
【解析】试题分析：先把x1=3代入关于x的一元二次方程﹣x2+2x+k=0，求出k的值，再根据根与系数的关系即可求出另一个解x2的值．
【解析】
∵把x1=3代入关于x的一元二次方程﹣x2+2x+k=0得，
﹣9+6+k=0，解得k=3，
∴原方程可化为：﹣x2+2x+3=0，
∴x1+x2=3+x2=﹣=2，解得x2=﹣1．
故选B． 将多项式-6a3b2-3a2b2+12a2b3分解因式时，应提取的公因式是（ ）
A．-3a2b2 B．-3ab C．-3a2b D．-3a3b3
A
【解析】
在找公因式时，一找系数的最大公约数，二找相同字母的最低次幂．同时注意首项系数通常要变成正数． 如图，MN表示某引水工程的一段设计路线，从点M到点N的走向为北偏西30°，在点M的北偏西60°方向上有一点A，以点A为圆心，以500米为半径的圆形区域为居民区，取MN上另一点B，测得BA的方向为北偏西75°．已知MB=400米，若不改变方向，则输水路线是否会穿过居民区？请通过计算说明理由．（参考数据：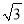 
≈1.732）
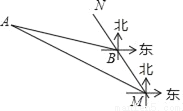
不会穿过居民区，理由见解析.
【解析】试题分析：要判断输水路线是否会穿过居民区，即要比较点A到MN的距离与500的大小，要求点A到MN的距离，作AD⊥MN交MN于点D，设AD=x，不难表示出DM=x+400，再由tan∠AMD==列出方程，解出x，比较x与500的大小，若x＞500，则不会穿过居民区；若x≤500，则会穿过居民区.
试题解析：
【解析】
过A作AD⊥MN于点D，...