题目内容
15. 如图,四边形ABCD外切于⊙O,已知AB=5,CD=11,AD=4,∠B=90°,则△ABC的外接圆半径为$\frac{13}{2}$.
如图,四边形ABCD外切于⊙O,已知AB=5,CD=11,AD=4,∠B=90°,则△ABC的外接圆半径为$\frac{13}{2}$.
分析 如图,根据切线的性质得到AE=AH,BE=BF,CF=CG,DH=DG,设AH=AE=x,得到DH=DG=4-x,BE=BF=5-x,求出BC=BF+CF=12,根据勾股定理得到AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=13,由∠B=90°,得到△ABC的外接圆是以AC为直径的圆,即可得到结论.
解答  解:如图,∵四边形ABCD外切于⊙O,
解:如图,∵四边形ABCD外切于⊙O,
设切点分别为E,F,G,H,
∴OE⊥AB,OF⊥BC,OG⊥CD,OH⊥AH,
∴AE=AH,BE=BF,CF=CG,DH=DG,
设AH=AE=x,
∴DH=DG=4-x,BE=BF=5-x,
∴CG=CF=7+x,
∴BC=BF+CF=12,
∵∠B=90°,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=13,
∵∠B=90°,
∴△ABC的外接圆是以AC为直径的圆,
∴△ABC的外接圆半径=$\frac{AC}{2}$=$\frac{13}{2}$,
故答案为:$\frac{13}{2}$.
点评 本题考查了切线的性质,四边形的内切圆和外接圆,勾股定理,熟练掌握切线的性质是解题的关键.

练习册系列答案
相关题目
3. 如图,若∠ABC=90°,∠ABE=∠CBD,则∠DBE等于( )
如图,若∠ABC=90°,∠ABE=∠CBD,则∠DBE等于( )
 如图,若∠ABC=90°,∠ABE=∠CBD,则∠DBE等于( )
如图,若∠ABC=90°,∠ABE=∠CBD,则∠DBE等于( )| A. | 60° | B. | 80° | C. | 90° | D. | 100° |
10. 如图,BC是⊙O的直径,点B、C、E、D都在⊙O上,则$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=( )
如图,BC是⊙O的直径,点B、C、E、D都在⊙O上,则$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=( )
 如图,BC是⊙O的直径,点B、C、E、D都在⊙O上,则$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=( )
如图,BC是⊙O的直径,点B、C、E、D都在⊙O上,则$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=( )| A. | sinA | B. | sin2A | C. | cosA | D. | cos2A |
20.观察如图图形的构成规律,根据此规律,第n个图形中圆的个数是( )


| A. | n2-1 | B. | n2 | C. | n2+2n | D. | n2+1 |
4. 某市努力改善空气质量,近年来空气质量明显好转,根据该市环保局公布的2010-2014这五年各年的空气质量:优良的天数,绘制成如图折线图,则这五年的全年空气质量优良天数平均为( )
某市努力改善空气质量,近年来空气质量明显好转,根据该市环保局公布的2010-2014这五年各年的空气质量:优良的天数,绘制成如图折线图,则这五年的全年空气质量优良天数平均为( )
 某市努力改善空气质量,近年来空气质量明显好转,根据该市环保局公布的2010-2014这五年各年的空气质量:优良的天数,绘制成如图折线图,则这五年的全年空气质量优良天数平均为( )
某市努力改善空气质量,近年来空气质量明显好转,根据该市环保局公布的2010-2014这五年各年的空气质量:优良的天数,绘制成如图折线图,则这五年的全年空气质量优良天数平均为( )| A. | 343天 | B. | 344天 | C. | 345天 | D. | 346天 |
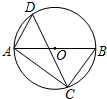 如图,AB为⊙O的直径,CD是⊙O的弦,∠ADC=54°,则∠BAC=36°.
如图,AB为⊙O的直径,CD是⊙O的弦,∠ADC=54°,则∠BAC=36°. 如图,已知AC,BC分别平分∠QAB,∠ABN,且∠1与∠2互余,求证:PQ∥MN.
如图,已知AC,BC分别平分∠QAB,∠ABN,且∠1与∠2互余,求证:PQ∥MN.