题目内容
10. 如图,BC是⊙O的直径,点B、C、E、D都在⊙O上,则$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=( )
如图,BC是⊙O的直径,点B、C、E、D都在⊙O上,则$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=( )| A. | sinA | B. | sin2A | C. | cosA | D. | cos2A |
分析 连接CD,由BC是⊙O的直径,得到∠ADC=∠BDC=90°,通过△ADE∽△ACB,得到$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=($\frac{AD}{AC}$)2=cos2A.
解答  解:连接CD,
解:连接CD,
∵BC是⊙O的直径,
∴∠ADC=∠BDC=90°,
∵点B、C、E、D都在⊙O上,
∴∠AED=∠B,
∵∠A=∠A,
∴△ADE∽△ACB,
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=($\frac{AD}{AC}$)2=cos2A,
故选D.
点评 本题考查了相似三角形的判定和性质,圆内接四边形的性质,圆周角定理,三角函数的定义,正确的作出辅助线是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.下列各点中,在函数y=-$\frac{4}{x}$图象上的是( )
| A. | (-1,4) | B. | (2,2) | C. | (-1,-4) | D. | (4,1) |
5.教室里的饮水机接通电源就进入自动程序,开机加热时水温上升,加热到100℃停止加热,水温开始下降,水温降至30℃,饮水机自动开始加热,重复上述程序.值日生小明7点钟到校后接通饮水机电源,在水温下降的过程中进行了水温检测,记录如下表:
(1)在图中的平面直角坐标系,画出水温y关于饮水机接通电源时间x的函数图象;
(2)借助(1)所画的图象,判断从7:00开始加温到水温第一次降到30℃为止,水温y和时间x之间存在怎样的函数关系?试求出函数关系并写出自变量x取值范围;
(3)上午第一节下课时间为8:25,同学们能不能喝到不超过50℃的水?请通过计算说明.
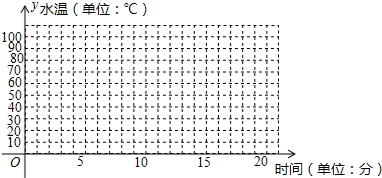
| 时间x | 7:00 | 7:02 | 7:05 | 7:07 | 7:10 | 7:14 | 7:20 |
| 水温y | 30℃ | 50℃ | 80℃ | 100℃ | 70℃ | 50℃ | 35℃ |
(2)借助(1)所画的图象,判断从7:00开始加温到水温第一次降到30℃为止,水温y和时间x之间存在怎样的函数关系?试求出函数关系并写出自变量x取值范围;
(3)上午第一节下课时间为8:25,同学们能不能喝到不超过50℃的水?请通过计算说明.

19. 如图所示,有理数a、b在数轴上的位置如图,则下列说法错误的是( )
如图所示,有理数a、b在数轴上的位置如图,则下列说法错误的是( )
 如图所示,有理数a、b在数轴上的位置如图,则下列说法错误的是( )
如图所示,有理数a、b在数轴上的位置如图,则下列说法错误的是( )| A. | b-a>0 | B. | a+b<0 | C. | ab<0 | D. | b<a |
20.已知多项式ax+b与2x2-x+2的乘积展开式中不含x的一次项,且常数项为-4,则ab的值为( )
| A. | -2 | B. | 2 | C. | -1 | D. | 1 |
 如图,四边形ABCD外切于⊙O,已知AB=5,CD=11,AD=4,∠B=90°,则△ABC的外接圆半径为$\frac{13}{2}$.
如图,四边形ABCD外切于⊙O,已知AB=5,CD=11,AD=4,∠B=90°,则△ABC的外接圆半径为$\frac{13}{2}$.