题目内容
6．
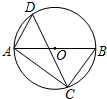如图，AB为⊙O的直径，CD是⊙O的弦，∠ADC=54°，则∠BAC=36°．
分析 根据圆周角定理得到∠B=∠ADC=54°，∠ACB=90°，根据三角形内角和定理计算即可．
解答 解：由圆周角定理得，∠B=∠ADC=54°，
∵AB为⊙O的直径，
∴∠ACB=90°，
∴∠BAC=90°-∠B=36°，
故答案为：36．
点评 本题考查的是圆周角定理的应用，掌握在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半和半圆（或直径）所对的圆周角是直角是解题的关键．
练习册系列答案
优生乐园系列答案
相关题目
某菜农搭建了一个横截面为抛物线的大棚，尺寸如图：
17．一个不透明的口袋中装有3个黑球和5个白球，这些球的大小、质地完全相同，从口袋中随机摸出1个球，这个球是黑球的概率是（ ）
| A． | $\frac{1}{8}$ | B． | $\frac{3}{8}$ | C． | $\frac{5}{8}$ | D． | $\frac{7}{8}$ |
14．若（m-2016）2+（2014-m）2=2，则（2014-m）（m-2016）=（ ）
| A． | 2015 | B． | 2016 | C． | 1 | D． | 2 |
1．下列各点中，在函数y=-$\frac{4}{x}$图象上的是（ ）
| A． | （-1，4） | B． | （2，2） | C． | （-1，-4） | D． | （4，1） |
如图，四边形ABCD外切于⊙O，已知AB=5，CD=11，AD=4，∠B=90°，则△ABC的外接圆半径为$\frac{13}{2}$．