题目内容
若△ABC的三边长分别为a,b,c,根据条件a3-a2c-ab2+abc=0,判断△ABC的形状.
考点:因式分解的应用
专题:
分析:首先观察所给等式左边代数式的结构特点,然后分组分解;结合三角形的三边关系判断出a-b=0,即可解决问题.
解答:解:∵a3-a2c-ab2+abc=0,
∴a3-ab2-(a2c-abc)=0,
即a(a+b)(a-b)-ac(a-b)=0,
∴(a-b)[a(a+b)-ac]=0;
∵a+b>c,
∴a(a+b)>ac,即a(a+b)-ac>0,
∴必有a-b=0,即 a=b,
∴△ABC是等腰三角形.
∴a3-ab2-(a2c-abc)=0,
即a(a+b)(a-b)-ac(a-b)=0,
∴(a-b)[a(a+b)-ac]=0;
∵a+b>c,
∴a(a+b)>ac,即a(a+b)-ac>0,
∴必有a-b=0,即 a=b,
∴△ABC是等腰三角形.
点评:该题主要考查了因式分解及其应用问题;解题的关键是牢固掌握掌握分组分解法或提公因式法,灵活选用有关方法来变形、化简、求值或证明.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
若在同一个坐标系中作出下列直线:①y=-
x-1;②y=2x-1;③y=-
x+1;④y=x-1,那么相互平行直线是( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、①③ | B、②④ | C、①② | D、①④ |
 如图,△ABC绕点A顺时针旋转60°得到△AEF,若∠B=100°,∠F=50°,则∠CAE的度数为
如图,△ABC绕点A顺时针旋转60°得到△AEF,若∠B=100°,∠F=50°,则∠CAE的度数为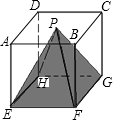 一个边长为5厘米的正方体,它是由125个边长为1厘米的小正方体组成的,P为上底面ABCD的中心,如果挖去的阴影部分为四棱锥,剩下的部分还包括多少个完整的棱长是1厘米的小正方体?
一个边长为5厘米的正方体,它是由125个边长为1厘米的小正方体组成的,P为上底面ABCD的中心,如果挖去的阴影部分为四棱锥,剩下的部分还包括多少个完整的棱长是1厘米的小正方体?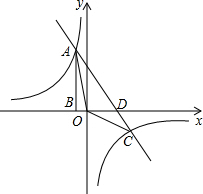 如图,点A是双曲线
如图,点A是双曲线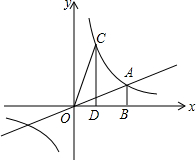 如图,直线y=
如图,直线y=