Question

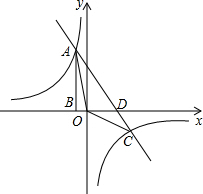如图，点A是双曲线y=

k

x

与直线y=-x-（k+1）在第二象限内的交点，AB⊥x轴于B，且S_△ABO=

5

2

．
（1）求这两个函数的解析式；
（2）求直线与双曲线的两个交点A、C的坐标和△AOC的面积；
（3）写出当一次函数值大于反比例函数值时，x取值范围？

Answer 1

考点：反比例函数与一次函数的交点问题

专题：

分析：（1）设出点A的坐标，根据面积公式求出坐标即可解决问题．
（2）联立方程组，解方程组得A、C两点的坐标；求出点D的坐标，即可解决问题．
（3）观察函数图象，即可解决问题．

解答：解：（1）设点A的坐标为（λ，μ），
则μ=

k

λ

，μ=-λ-(k+1)；
∵点A在第二象限，
∴AB=μ，OB=-λ，
∵S_△ABO=

5

2

，即

1

2

(-λ)μ=

5

2

，
∴λμ=-5，k=λμ=-5，
两个函数的解析式为：y=-

5

x

，y=-x+4．
（2）解方程组

y=- 5 x y=-x+4

得：

x=5 y=-1

，

x=-1 y=5

，
∴A、C两点的坐标分别为A（-1，5），C（5，-1）；
对于直线AC，当x=0时，y=4，即OD=4；
S_△AOC=S_△AOD+S_△COD
=

1

2

×4×5+

1

2

×4×1=12，
即△AOC的面积=12．
（3）由图象知：当一次函数值大于反比例函数值时，
x取值范围是：x＜-1或0＜x＜5．

点评：该题主要考查了反比例函数的图象与一次函数的图象的交点问题；解题的关键是数形结合，灵活运用方程等代数知识来分析、判断、求解或证明．