题目内容
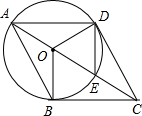 已知:如图,AE是⊙O的直径,C是AE延长线上的点,且EC=
已知:如图,AE是⊙O的直径,C是AE延长线上的点,且EC=| 1 |
| 2 |
(1)四边形ABCD是菱形吗?为什么?
(2)试说明CD是⊙O的切线.
考点:切线的判定,菱形的判定
专题:
分析:(1)根据切线的性质,由CB与⊙O相切于点B得到OB⊥BC,在利用AE是⊙O的直径,EC=
AE得到OE=CE,在Rt△OBC中,由于OB=
OC,根据含30度的直角三角形三边的关系得到∠BCO=30°,∠BOC=60°,则BC=
OB,接着利用三角形外角性质得∠BOC=∠OAB+∠OBC,可计算出∠OAB=30°,所以BA=BC,再利用AD∥BC得到∠DAC=∠BCA=30°,然后由AE是⊙O的直径得到∠ADE=90°,所以DE=
AE,即DE=OD,AD=
DE=
OD,因此AD=BC,则可判断四边形ABCD为平行四边形,加上BA=BC,则可判断四边形ABCD是菱形;
(2)由四边形ABCD是菱形得到CB=CD,再证明△OBC≌△ODC得到∠OBC=∠ODC=90°,于是根据切线的判定定理可得CD是⊙O的切线.
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
(2)由四边形ABCD是菱形得到CB=CD,再证明△OBC≌△ODC得到∠OBC=∠ODC=90°,于是根据切线的判定定理可得CD是⊙O的切线.
解答:解:(1)四边形ABCD是菱形.理由如下:
∵CB与⊙O相切于点B,
∴OB⊥BC,
∵AE是⊙O的直径,EC=
AE,
∴OE=CE,
在Rt△OBC中,∵OB=
OC,
∴∠BCO=30°,∠BOC=60°,BC=
OB,
而∠BOC=∠OAB+∠OBC,
∴∠OAB=30°,
∴BA=BC,
∵AD∥BC,
∴∠DAC=∠BCA=30°,
∵AE是⊙O的直径,
∴∠ADE=90°,
∴DE=
AE,即DE=OD,
∴AD=
DE=
OD,
∴AD=BC,
而AD∥BC,
∴四边形ABCD为平行四边形,
而BA=BC,
∴四边形ABCD是菱形;
(2)CD是⊙O的切线.理由如下:
∵四边形ABCD是菱形,
∴CB=CD,
在△OBC和△ODC中,
,
∴△OBC≌△ODC,
∴∠OBC=∠ODC=90°,
∴OD⊥DC,
∴CD是⊙O的切线.
∵CB与⊙O相切于点B,
∴OB⊥BC,
∵AE是⊙O的直径,EC=
| 1 |
| 2 |
∴OE=CE,
在Rt△OBC中,∵OB=
| 1 |
| 2 |
∴∠BCO=30°,∠BOC=60°,BC=
| 3 |
而∠BOC=∠OAB+∠OBC,
∴∠OAB=30°,
∴BA=BC,
∵AD∥BC,
∴∠DAC=∠BCA=30°,
∵AE是⊙O的直径,
∴∠ADE=90°,
∴DE=
| 1 |
| 2 |
∴AD=
| 3 |
| 3 |
∴AD=BC,
而AD∥BC,
∴四边形ABCD为平行四边形,
而BA=BC,
∴四边形ABCD是菱形;
(2)CD是⊙O的切线.理由如下:
∵四边形ABCD是菱形,
∴CB=CD,
在△OBC和△ODC中,
|
∴△OBC≌△ODC,
∴∠OBC=∠ODC=90°,
∴OD⊥DC,
∴CD是⊙O的切线.
点评:本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线;在判定一条直线为圆的切线时,当已知条件中未明确指出直线和圆是否有公共点时,常过圆心作该直线的垂线段,证明该线段的长等于半径;当已知条件中明确指出直线与圆有公共点时,常连接过该公共点的半径,证明该半径垂直于这条直线.也考查了菱形的判定.

练习册系列答案
相关题目
 如图,∠AOB=60°,∠AOC=90°,OB是∠AOD的平分线,求∠COD的度数.
如图,∠AOB=60°,∠AOC=90°,OB是∠AOD的平分线,求∠COD的度数.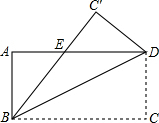 如图,将长方形ABCD沿BD对折,C点落在C′的位置,BC′与AD交于点E.
如图,将长方形ABCD沿BD对折,C点落在C′的位置,BC′与AD交于点E.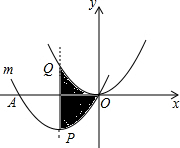 如图,把抛物线y=x2平移得到抛物线m,抛物线m经过点A(-4,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=x2交于点Q,则图中阴影部分的面积为
如图,把抛物线y=x2平移得到抛物线m,抛物线m经过点A(-4,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=x2交于点Q,则图中阴影部分的面积为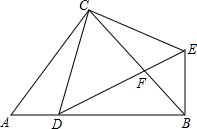 如图,在△ABC中,∠ACB=90°,CA=CB,点D为AB上一点,CE⊥CD于C,且CE=CD,连接BE、DE,DE与BC交于点F.
如图,在△ABC中,∠ACB=90°,CA=CB,点D为AB上一点,CE⊥CD于C,且CE=CD,连接BE、DE,DE与BC交于点F. 如图:图中射线有
如图:图中射线有