题目内容
求下列二次函数的图象与x轴交点的坐标,并作草图验证:
(1)y=x2-3x-5
(2)y=-3x2+22x-24.
(1)y=x2-3x-5
(2)y=-3x2+22x-24.
考点:抛物线与x轴的交点
专题:
分析:分别令y=0得到关于x的一元二次方程,求方程的解可得与x轴交点的坐标,画出草图即可.
解答:解:(1)令y=0可得:x2-3x-5=0,解得x=
,
所以二次函数y=x2-3x-5与x轴的交点坐标为(
,0)和(
,0);
如图1:

(2)令y=0可得:-3x2+22x-24=0,解得x=6或
,
所以二次函数y=-3x2+22x-24与x轴的交点坐标为(6,0)和(
,0),
如图2:

3±
| ||
| 2 |
所以二次函数y=x2-3x-5与x轴的交点坐标为(
3+
| ||
| 2 |
3-
| ||
| 2 |
如图1:

(2)令y=0可得:-3x2+22x-24=0,解得x=6或
| 4 |
| 3 |
所以二次函数y=-3x2+22x-24与x轴的交点坐标为(6,0)和(
| 4 |
| 3 |
如图2:

点评:本题主要考查二次函数与x轴的交点,掌握二次函数图象与x轴的交点的横坐标是对应的一元二次方程的两根是解题的关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
 如图,AC=
如图,AC=| 1 |
| 3 |
| 1 |
| 4 |
| A、1:6 | B、1:8 |
| C、1:12 | D、1:16 |
 甲、乙二人沿着相同的路线由A地到B地匀速行进.已知A、B两地间的路程为20km,他们行进的路程s(km)与行进的时间t(h)之间的函数关系如图所示.根据图象信息,下列说法不正确的是( )
甲、乙二人沿着相同的路线由A地到B地匀速行进.已知A、B两地间的路程为20km,他们行进的路程s(km)与行进的时间t(h)之间的函数关系如图所示.根据图象信息,下列说法不正确的是( )| A、甲的速度是5km/h |
| B、乙的速度是20km/h |
| C、乙比甲晚出发1h |
| D、甲走完全程比乙走完全程多用了2h |
从O点看,射线OA在是北偏西60°方向上,射线OB在南偏东15°方向上,那么∠AOB的度数为( )
| A、45° | B、75° |
| C、90° | D、135° |
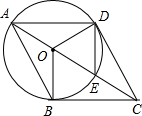 已知:如图,AE是⊙O的直径,C是AE延长线上的点,且EC=
已知:如图,AE是⊙O的直径,C是AE延长线上的点,且EC=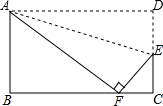 如图,将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上F点处,已知CE=6,AB=16,则BF=
如图,将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上F点处,已知CE=6,AB=16,则BF= 在△ABC中,AB=AC.D为△ABC外一点,且∠ABD=∠ACD=60°.求证:CD=AB-BD.
在△ABC中,AB=AC.D为△ABC外一点,且∠ABD=∠ACD=60°.求证:CD=AB-BD.