题目内容
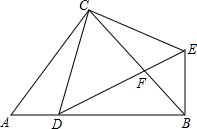 如图,在△ABC中,∠ACB=90°,CA=CB,点D为AB上一点,CE⊥CD于C,且CE=CD,连接BE、DE,DE与BC交于点F.
如图,在△ABC中,∠ACB=90°,CA=CB,点D为AB上一点,CE⊥CD于C,且CE=CD,连接BE、DE,DE与BC交于点F.(1)求证:BE⊥AB;
(2)若∠ACD=30°,求证:DE=2AD.
考点:全等三角形的判定与性质
专题:证明题
分析:(1)证明∠ACD=∠BCE,此为解决问题的关键性结论;证明△ADC≌△BEC,得到∠CBE=∠A=45°,即可解决问题.
(2)证明C、D、B、E四点共圆,得到∠EDB=∠BCE;证明∠ACD=∠BCE=30°,即可解决问题.
(2)证明C、D、B、E四点共圆,得到∠EDB=∠BCE;证明∠ACD=∠BCE=30°,即可解决问题.
解答: 解:(1)∵∠ACB=90°,CE⊥CD,
解:(1)∵∠ACB=90°,CE⊥CD,
∴∠ACB=∠DCE,
∴∠ACD=∠BCE;
∵∠ACB=90°,AC=BC,
∴∠A=∠ABC=45°;
在△ADC与△BEC中,
,
∴△ADC≌△BEC(SAS),
∴∠CBE=∠A=45°,
∴∠DBE=90°,即BE⊥AB.
(2)∵∠CDE=∠CBE=45°,
∴C、D、B、E四点共圆,
∴∠EDB=∠BCE;
∵∠ACD=∠BCE=30°,
∴∠EDB=30°,DE=2BE;
∵△ADC≌△BEC,
∴AD=BE,DE=2AD.
 解:(1)∵∠ACB=90°,CE⊥CD,
解:(1)∵∠ACB=90°,CE⊥CD,∴∠ACB=∠DCE,
∴∠ACD=∠BCE;
∵∠ACB=90°,AC=BC,
∴∠A=∠ABC=45°;
在△ADC与△BEC中,
|
∴△ADC≌△BEC(SAS),
∴∠CBE=∠A=45°,
∴∠DBE=90°,即BE⊥AB.
(2)∵∠CDE=∠CBE=45°,
∴C、D、B、E四点共圆,
∴∠EDB=∠BCE;
∵∠ACD=∠BCE=30°,
∴∠EDB=30°,DE=2BE;
∵△ADC≌△BEC,
∴AD=BE,DE=2AD.
点评:该题主要考查了全等三角形的判定及其性质的应用问题;解题的关键是灵活运用有关定理来分析、判断、推理或解答;对综合的分析问题解决问题的能力提出了较高的要求.

练习册系列答案
相关题目
 如图,已知∠AOB是直角,OM平分∠AOC,ON平分∠BOC,则∠MON的度数是( )
如图,已知∠AOB是直角,OM平分∠AOC,ON平分∠BOC,则∠MON的度数是( )| A、60° | B、50° |
| C、45° | D、30° |
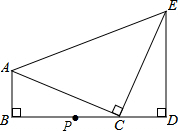 如图,点AB⊥BD于点B,ED⊥BD于点D,点C在BD上,且∠ACE=90°,AC=CE,AB=4,BC=6.
如图,点AB⊥BD于点B,ED⊥BD于点D,点C在BD上,且∠ACE=90°,AC=CE,AB=4,BC=6. 如图,BE、CF是△ABC的两条高,它们相交于点Q,CQ=AB,连结AQ,延长BE到P,使BP=AC.
如图,BE、CF是△ABC的两条高,它们相交于点Q,CQ=AB,连结AQ,延长BE到P,使BP=AC. 如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的直线互相垂直,垂足为D,且AC平分∠DAB.
如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的直线互相垂直,垂足为D,且AC平分∠DAB.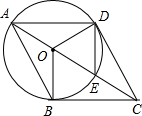 已知:如图,AE是⊙O的直径,C是AE延长线上的点,且EC=
已知:如图,AE是⊙O的直径,C是AE延长线上的点,且EC= 在△ABC中,AB=AC.D为△ABC外一点,且∠ABD=∠ACD=60°.求证:CD=AB-BD.
在△ABC中,AB=AC.D为△ABC外一点,且∠ABD=∠ACD=60°.求证:CD=AB-BD.