题目内容
已知抛物线y=x2-x+c,当-1<x<3时,抛物线与x轴有公共点,求c的取值范围.
考点:抛物线与x轴的交点
专题:
分析:可先把抛物线化为顶点式,求得其顶点坐标,且其对称轴在所给范围之内,只需要其最小值小于或等于0即可.
解答:解:
∵y=x2-x+c=(x-
)2+c-
,
∴其对称轴为x=-
,最小值c-
,
∵当-1<x<3时,抛物线与x轴有公共点,
∴其最小值小于或等于0,
∴c-
≤0,解得c≤
.
∵y=x2-x+c=(x-
| 1 |
| 2 |
| 1 |
| 4 |
∴其对称轴为x=-
| 1 |
| 2 |
| 1 |
| 4 |
∵当-1<x<3时,抛物线与x轴有公共点,
∴其最小值小于或等于0,
∴c-
| 1 |
| 4 |
| 1 |
| 4 |
点评:本题主要考查二次函数的对称轴、顶点坐标,确定出当-1<x<3时,抛物线与x轴有公共点所满足的条件是解题的关键,注意结合图形来理解.

练习册系列答案
相关题目
 如图,AC=
如图,AC=| 1 |
| 3 |
| 1 |
| 4 |
| A、1:6 | B、1:8 |
| C、1:12 | D、1:16 |
 已知:如图,在平面直角坐标xOy中,边长为2的等边△OAB的顶点B在第一象限,顶点A在x轴的正半轴上.另一等腰△OCA的顶点C在第四象限,OC=AC,∠C=120°.现有两动点P、Q分别从A、O两点同时出发,点Q以每秒1个单位的速度沿OC向点C运动,点P以每秒3个单位的速度沿A→O→B运动,当其中一个点到达终点时,另一个点也随即停止.
已知:如图,在平面直角坐标xOy中,边长为2的等边△OAB的顶点B在第一象限,顶点A在x轴的正半轴上.另一等腰△OCA的顶点C在第四象限,OC=AC,∠C=120°.现有两动点P、Q分别从A、O两点同时出发,点Q以每秒1个单位的速度沿OC向点C运动,点P以每秒3个单位的速度沿A→O→B运动,当其中一个点到达终点时,另一个点也随即停止. 如图,在△ABC中,点C,F分别在上BD、AB上.AC、DF相交于E.若CD=2BC,AE=2CE,则DE:EF=
如图,在△ABC中,点C,F分别在上BD、AB上.AC、DF相交于E.若CD=2BC,AE=2CE,则DE:EF= △ABC中,AB⊥BC,AB=BC,E为BC上一点,连接AE,过点C作CF⊥AE交AE的延长线于点F,连接BF,过点B作BG⊥BF交AE于G.
△ABC中,AB⊥BC,AB=BC,E为BC上一点,连接AE,过点C作CF⊥AE交AE的延长线于点F,连接BF,过点B作BG⊥BF交AE于G.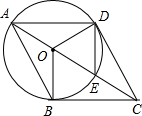 已知:如图,AE是⊙O的直径,C是AE延长线上的点,且EC=
已知:如图,AE是⊙O的直径,C是AE延长线上的点,且EC=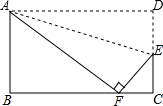 如图,将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上F点处,已知CE=6,AB=16,则BF=
如图,将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上F点处,已知CE=6,AB=16,则BF=