题目内容
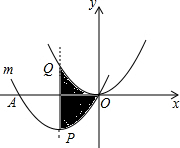 如图,把抛物线y=x2平移得到抛物线m,抛物线m经过点A(-4,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=x2交于点Q,则图中阴影部分的面积为
如图,把抛物线y=x2平移得到抛物线m,抛物线m经过点A(-4,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=x2交于点Q,则图中阴影部分的面积为考点:二次函数图象与几何变换
专题:计算题
分析:连结OQ、OP,如图,先利用交点时写出平移后的抛物线m的解析式,再用配方得到顶点式y=(x+2)2-4,则P点坐标为(-2,-4),抛物线m的对称轴为直线x=-2,于是可计算出
Q点的坐标为(-2,4),所以点Q与P点关于x轴对称,于是得到图中阴影部分的面积,然后根据三角形面积公式计算.
Q点的坐标为(-2,4),所以点Q与P点关于x轴对称,于是得到图中阴影部分的面积,然后根据三角形面积公式计算.
解答:解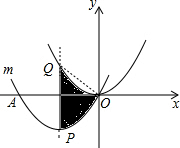 :连结OQ、OP,如图,
:连结OQ、OP,如图,
平移后的抛物线解析式为y=(x+4)•x=x2+4x=(x+2)2-4,
所以P点坐标为(-2,-4),
抛物线m的对称轴为直线x=-2,
当x=-2时,y=x2=4,则Q点的坐标为(-2,4),
由于抛物线y=x2向左平移2个单位,再向下平移4个单位得到抛物线y=(x+2)2-4,
所以图中阴影部分的面积=S△OPQ=
×2×(4+4)=8.
故答案为8.
 :连结OQ、OP,如图,
:连结OQ、OP,如图,平移后的抛物线解析式为y=(x+4)•x=x2+4x=(x+2)2-4,
所以P点坐标为(-2,-4),
抛物线m的对称轴为直线x=-2,
当x=-2时,y=x2=4,则Q点的坐标为(-2,4),
由于抛物线y=x2向左平移2个单位,再向下平移4个单位得到抛物线y=(x+2)2-4,
所以图中阴影部分的面积=S△OPQ=
| 1 |
| 2 |
故答案为8.
点评:本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.

练习册系列答案
相关题目
从O点看,射线OA在是北偏西60°方向上,射线OB在南偏东15°方向上,那么∠AOB的度数为( )
| A、45° | B、75° |
| C、90° | D、135° |
 如图,在三角形ABC中,点D,E,F分别在BC,AB,AC上,BD=CF,BE=CD,AB=AC,DG⊥EF于点G,求证:EG=FG.
如图,在三角形ABC中,点D,E,F分别在BC,AB,AC上,BD=CF,BE=CD,AB=AC,DG⊥EF于点G,求证:EG=FG. 如图,在△ABC中,点C,F分别在上BD、AB上.AC、DF相交于E.若CD=2BC,AE=2CE,则DE:EF=
如图,在△ABC中,点C,F分别在上BD、AB上.AC、DF相交于E.若CD=2BC,AE=2CE,则DE:EF= 如图,BE、CF是△ABC的两条高,它们相交于点Q,CQ=AB,连结AQ,延长BE到P,使BP=AC.
如图,BE、CF是△ABC的两条高,它们相交于点Q,CQ=AB,连结AQ,延长BE到P,使BP=AC. △ABC中,AB⊥BC,AB=BC,E为BC上一点,连接AE,过点C作CF⊥AE交AE的延长线于点F,连接BF,过点B作BG⊥BF交AE于G.
△ABC中,AB⊥BC,AB=BC,E为BC上一点,连接AE,过点C作CF⊥AE交AE的延长线于点F,连接BF,过点B作BG⊥BF交AE于G.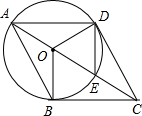 已知:如图,AE是⊙O的直径,C是AE延长线上的点,且EC=
已知:如图,AE是⊙O的直径,C是AE延长线上的点,且EC=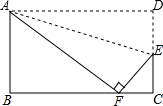 如图,将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上F点处,已知CE=6,AB=16,则BF=
如图,将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上F点处,已知CE=6,AB=16,则BF=