题目内容
有一列数,第一的数为4,第二个数为7,…且从第二个数至第n-1个数,每个数是它相邻的两个数和的平均数少1,则这列数中的第n个数为 .
考点:规律型:数字的变化类
专题:
分析:先根据题意分别计算出第三个数为2×7-4=10;第四个数为2×10-7=13;第五个数为2×13-10=16;…由此得到这列数的后面一个数比它前面的数大3,即4,7,10,13,16,…,则得到第n个数为1+3n.
解答:解:第一个数是4;
第二个数7;
而从第二个数开始,每个数是它相邻两数和的一半,
第三个数为2×7-4=10;
第四个数为2×10-7=13;
第五个数为2×13-10=16;
…
第n个数为1+3n.
故答案为:3n+1.
第二个数7;
而从第二个数开始,每个数是它相邻两数和的一半,
第三个数为2×7-4=10;
第四个数为2×10-7=13;
第五个数为2×13-10=16;
…
第n个数为1+3n.
故答案为:3n+1.
点评:本题考查了数字的变化规律,通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素,然后推广到一般情况.

练习册系列答案
相关题目
下列正确的选项是( )
①线段AB和线段BA是同一条线段.②射线AB和射线BA是同一条射线.③直线AB和直线BA式同一条直线.④线段BA和射线AB,都是直线AB的一部分.
①线段AB和线段BA是同一条线段.②射线AB和射线BA是同一条射线.③直线AB和直线BA式同一条直线.④线段BA和射线AB,都是直线AB的一部分.
| A、①②③ | B、①③④ |
| C、③④ | D、①②③④ |
 甲、乙二人沿着相同的路线由A地到B地匀速行进.已知A、B两地间的路程为20km,他们行进的路程s(km)与行进的时间t(h)之间的函数关系如图所示.根据图象信息,下列说法不正确的是( )
甲、乙二人沿着相同的路线由A地到B地匀速行进.已知A、B两地间的路程为20km,他们行进的路程s(km)与行进的时间t(h)之间的函数关系如图所示.根据图象信息,下列说法不正确的是( )| A、甲的速度是5km/h |
| B、乙的速度是20km/h |
| C、乙比甲晚出发1h |
| D、甲走完全程比乙走完全程多用了2h |
 如图,BE、CF是△ABC的两条高,它们相交于点Q,CQ=AB,连结AQ,延长BE到P,使BP=AC.
如图,BE、CF是△ABC的两条高,它们相交于点Q,CQ=AB,连结AQ,延长BE到P,使BP=AC.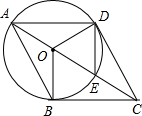 已知:如图,AE是⊙O的直径,C是AE延长线上的点,且EC=
已知:如图,AE是⊙O的直径,C是AE延长线上的点,且EC=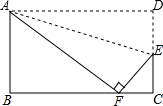 如图,将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上F点处,已知CE=6,AB=16,则BF=
如图,将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上F点处,已知CE=6,AB=16,则BF= 在△ABC中,AB=AC.D为△ABC外一点,且∠ABD=∠ACD=60°.求证:CD=AB-BD.
在△ABC中,AB=AC.D为△ABC外一点,且∠ABD=∠ACD=60°.求证:CD=AB-BD.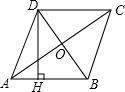 如图,菱形ABCD的对角线相交于点O,AC=16cm,周长为40cm,求菱形的高DH的长.
如图,菱形ABCD的对角线相交于点O,AC=16cm,周长为40cm,求菱形的高DH的长.