题目内容
10.解下列方程组:(1)$\left\{\begin{array}{l}y=2x-3\\ 3x+2y=8\end{array}$;
(2)$\left\{\begin{array}{l}\frac{x+y}{2}+\frac{x-y}{4}=-3\\ \frac{x+y}{2}-\frac{x-y}{4}=1\end{array}$.
分析 (1)方程组利用代入消元法求出解即可;
(2)方程组整理后,利用加减消元法求出解即可.
解答 解:(1)$\left\{\begin{array}{l}{y=2x-3①}\\{3x+2y=8②}\end{array}\right.$,
把①代入②得:3x+4x-6=8,即x=2,
把x=2代入①得:y=1,
则方程组的解为$\left\{\begin{array}{l}x=2\\ y=1\end{array}$;
(2)方程组整理得:$\left\{\begin{array}{l}{3x+y=-12①}\\{x+3y=4②}\end{array}\right.$,
①×3-②得:8x=-40,即x=-5,
把x=-5代入②得:y=3,
则方程组的解为$\left\{\begin{array}{l}x=-5\\ y=3\end{array}$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
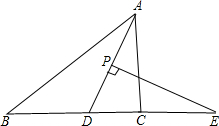 如图,在△ABC中,AD平分∠BAC,P为线段AD上的一个动点,PE⊥AD交直线BC于点E.
如图,在△ABC中,AD平分∠BAC,P为线段AD上的一个动点,PE⊥AD交直线BC于点E. 一个几何体的三视图如图所示,根据图示的数据计算该几何体的全面积为8$\sqrt{3}$+72.
一个几何体的三视图如图所示,根据图示的数据计算该几何体的全面积为8$\sqrt{3}$+72. 已知:如图,点B,F,C,E在一条直线上,BF=CE,AC=DF,且AC∥DF.求证:∠B=∠E.
已知:如图,点B,F,C,E在一条直线上,BF=CE,AC=DF,且AC∥DF.求证:∠B=∠E.