题目内容
15.用适当的方法解方程:(1)2(x+2)2-8=0;
(2)x(x-3)=x;
(3)x2+2x+3=0.
分析 (1)先把方程变形得到(x+2)2=4,然后利用直接开平方法解方程;
(2)先移项得到x(x-3)-x=0,然后利用因式分解法解方程;
(3)先计算判别式的值,然后根据判别式的意义判断方程无实数解.
解答 解:(1)(x+2)2=4,
x+2=±2,
所以x1=0,x2=-4;
(2)x(x-3)-x=0,
x(x-3-1)=0,
x=0或x-3-1=0,
所以x1=0,x2=4;
(3)△=22-4×1×4<0,
所以方程没有实数解.
点评 本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).也考查了直接开平方法和根的判别式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.观察下表多项式分解因式的特征,并回答问题.
对于二次项系数为1的二次三项式,若符合上述表中(2)(3)栏目的特征,就可以采用表中方法进行因式分解.
(1)分解因式:x2-4x-60;
(2)若x2+px-60可分解为两个一次因式的积,则整数p的值有12个.
| 1 | 2 | 3 | 4 |
| 多项式 | 常数项 | 一次项系数 | 分解因式 |
| x2+6x+8 | 8=2×4 | 6=2+4 | x2+6x+8=(x+2)(x+4) |
| x2-6x+8 | 8=(-2)×(-4) | -6=(-2)+(-4) | x2-6x+8=(x-2)(x-4) |
| x2+2x-8 | -8=4×(-2) | 2=4+(-2) | x2+2x-8=(x+4)(x-2) |
(1)分解因式:x2-4x-60;
(2)若x2+px-60可分解为两个一次因式的积,则整数p的值有12个.
5.某超市货架上摆放着外观、颜色、样式、规格完全相同的盒装酸奶,其生产日期有三盒是“20150410”,五盒是“20150412”,两盒是“20150413”.若从中随机抽取一盒,恰好抽到生产日期为“20150413”的概率是( )
| A. | $\frac{1}{10}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{5}$ |
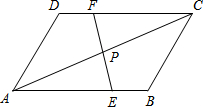 如图,?ABCD中,点E、F分别在AB、CD上,且BE=DF,EF与AC相交于点P,求证:PA=PC.
如图,?ABCD中,点E、F分别在AB、CD上,且BE=DF,EF与AC相交于点P,求证:PA=PC.