题目内容
2. 一个几何体的三视图如图所示,根据图示的数据计算该几何体的全面积为8$\sqrt{3}$+72.
一个几何体的三视图如图所示,根据图示的数据计算该几何体的全面积为8$\sqrt{3}$+72.
分析 根据三视图判断出该几何体的形状,再分别求出底面积和侧面积即可得出答案.
解答 解:根据三视图可得该几何体是一个三棱柱,底面积为$\frac{1}{2}$×4×$\sqrt{{4}^{2}-{2}^{2}}$=4$\sqrt{3}$,侧面积为4×3×6=72,
则该几何体的全面积为4$\sqrt{3}$×2+72=8$\sqrt{3}$+72,
故答案为:8$\sqrt{3}$+72.
点评 此题考查了由三视图判断几何体,用到的知识点是三角形、长方形的面积、勾股定理,同时也体现了对空间想象能力方面的考查.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
12.下列各式能用平方差公式计算的是( )
| A. | (x+2y)(x-2y) | B. | (a+b)(a-2b) | C. | (-a+2b)(a-2b) | D. | (-2m-n)(2m+n) |
 如图,矩形OBCD的顶点C的坐标为(1,3),则线段BD的长等于$\sqrt{10}$.
如图,矩形OBCD的顶点C的坐标为(1,3),则线段BD的长等于$\sqrt{10}$.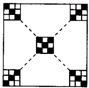 如图,用同样大小的正方形瓷砖铺一块正方形地面,两条对角线铺黑色,其他地方铺白色.铺满这块地面一共用了白色瓷砖100块,那么黑色瓷砖共用了21 块.
如图,用同样大小的正方形瓷砖铺一块正方形地面,两条对角线铺黑色,其他地方铺白色.铺满这块地面一共用了白色瓷砖100块,那么黑色瓷砖共用了21 块.