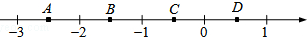题目内容
5.已知O为△ABC内角平分线的交点,OD⊥BC于D,∠A=60°,BC=2$\sqrt{3}$,则OD的最大值是1.分析 根据角平分线的交点到三角形三边的距离相等,可得OD是内切圆的半径,根据当△ABC为等边三角形时,内切圆的面积最大,即OD最大,求出此时的OD即可.
解答 解:由题意可知,点O为内心,
∴OD为内切圆的半径,
当△ABC为等边三角形时,内切圆的面积最大,即OD最大,
在等边△ABC中,∠A=60°,BC=2$\sqrt{3}$,
则OD=1,
故答案为:1.
点评 本题考查的是角平分线的性质:角平分线上的点到角的两边的距离相等和内心的概念,判断出当△ABC为等边三角形时,内切圆的面积最大,即OD最大是解题的关键.

练习册系列答案
相关题目
15.能判定四边形ABCD为平行四边形的条件是( )
| A. | AB=AD,CB=CD | B. | ∠A=∠B,∠C=∠D | C. | AB=CD,AD=BC | D. | AB∥CD,AD=BC |
 如图,矩形OBCD的顶点C的坐标为(1,3),则线段BD的长等于$\sqrt{10}$.
如图,矩形OBCD的顶点C的坐标为(1,3),则线段BD的长等于$\sqrt{10}$. 如图,小亮从A点出发前进5m,向右转15°,再前进5m,又向右转15°…,这样一直走下去,他第一次回到出发点A时,一共走了120m.
如图,小亮从A点出发前进5m,向右转15°,再前进5m,又向右转15°…,这样一直走下去,他第一次回到出发点A时,一共走了120m. 如图,用同样大小的正方形瓷砖铺一块正方形地面,两条对角线铺黑色,其他地方铺白色.铺满这块地面一共用了白色瓷砖100块,那么黑色瓷砖共用了21 块.
如图,用同样大小的正方形瓷砖铺一块正方形地面,两条对角线铺黑色,其他地方铺白色.铺满这块地面一共用了白色瓷砖100块,那么黑色瓷砖共用了21 块.