题目内容
19. 已知:如图,点B,F,C,E在一条直线上,BF=CE,AC=DF,且AC∥DF.求证:∠B=∠E.
已知:如图,点B,F,C,E在一条直线上,BF=CE,AC=DF,且AC∥DF.求证:∠B=∠E.
分析 先证出BC=EF,∠ACB=∠DFE,再证明△ACB≌△DFE,得出对应角相等即可.
解答 证明:∵BF=CE,
∴BC=EF,
∵AC∥DF,
∴∠ACB=∠DFE,
在△ACB和△DFE中,
$\left\{\begin{array}{l}{BC=EF}&{\;}\\{∠ACB=∠DFE}&{\;}\\{AC=DF}&{\;}\end{array}\right.$,
∴△ACB≌△DFE(SAS),
∴∠B=∠E.
点评 本题考查了全等三角形的判定与性质、平行线的性质;熟练掌握全等三角形的判定方法,证明三角形全等是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.某公司有5个股东,每个股东的利润相同,有100名工人,每名工人的工资相同.2015年第一个季度工人的工资总额与公司的股东总利润情况见表:
该公司老板根据表中数据,作出了图1,并声称股东利润和工人工资同步增长,公司和工人做到了“有福同享”.
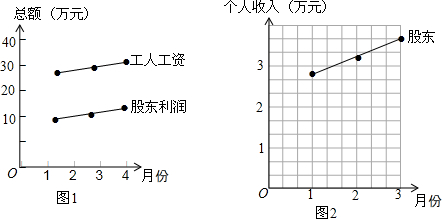
针对老板的说法,解决下列问题:
(1)这三个月工人个人的月收入分别是0.28,0.30,0.32万元;
(2)在图2中,已经做出这三个月每个股东利润统计图,请你补出这三个月工人个人月收入的统计图;
(3)通过完成第(1),(2)问和对图2的观察,你如何看待老板的说法?(用一两句话概括)
| 月份 | 工人工资总额(万元) | 股东总利润(万元) |
| 1 | 28 | 14 |
| 2 | 30 | 16 |
| 3 | 32 | 18 |

针对老板的说法,解决下列问题:
(1)这三个月工人个人的月收入分别是0.28,0.30,0.32万元;
(2)在图2中,已经做出这三个月每个股东利润统计图,请你补出这三个月工人个人月收入的统计图;
(3)通过完成第(1),(2)问和对图2的观察,你如何看待老板的说法?(用一两句话概括)
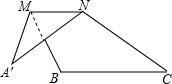 如图,将△ABC沿它的中位线MN折叠后,点A落在点A′处,若∠A=30°,∠B=115°,则∠A′NC=110°.
如图,将△ABC沿它的中位线MN折叠后,点A落在点A′处,若∠A=30°,∠B=115°,则∠A′NC=110°. 如图,在梯形ABCD中,AD∥BC,若△AOB的面积为8cm2,那么△DOC的面积为多少?
如图,在梯形ABCD中,AD∥BC,若△AOB的面积为8cm2,那么△DOC的面积为多少?