题目内容
20．在平面直角坐标系中，二次函数y=x2+ax+b的图象与x轴交于两点，且两交点之间的距离是4，若此函数图象的对称轴为x=-5，则此图象经过下列（ ）| A． | （-6，-4） | B． | （-6，-3） | C． | （-6，-2） | D． | （-6，-1） |
分析 直接利用两交点之间的距离是4，函数图象的对称轴为x=-5，得出图象与x轴交点，进而得出函数解析式，再利用x=-6求出答案．
解答 解：∵二次函数y=x2+ax+b的图象与x轴交于两点，且两交点之间的距离是4，若此函数图象的对称轴为x=-5，
∴图象与x轴的交点坐标为：（-3，0），（-7，0），
故y=（x+3）（x+7），
当x=-6时，y=-3×1=-3，
故此图象经过（-6，-3）．
故选：B．
点评 此题主要考查了抛物线与x轴交点，正确得出图象与x轴的交点坐标是解题关键．
练习册系列答案
相关题目
10．
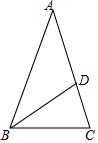如图，△ABC中，AB=AC，∠A=30°，以B为圆心，以BC为半径画弧交AC于点D，那么∠DBC的度数是（ ）
如图，△ABC中，AB=AC，∠A=30°，以B为圆心，以BC为半径画弧交AC于点D，那么∠DBC的度数是（ ）| A． | 30° | B． | 45° | C． | 40° | D． | 60° |
11．山东全省2016年国庆假期旅游人数增长12.5%，其中尤其是乡村旅游最为火爆．泰山脚下的某旅游村，为接待游客住宿需要，开设了有100张床位的旅馆，当每张床位每天收费100元时，床位可全部租出，若每张床位每天收费提高20元，则相应的减少了10张床位租出，如果每张床位每天以20元为单位提高收费，为使租出的床位少且租金高，那么每张床位每天最合适的收费是（ ）
| A． | 140元 | B． | 150元 | C． | 160元 | D． | 180元 |
8．用反证法证明命题：“△ABC中，若AB=AC，则∠B、∠C都是锐角”首先应假设（ ）
| A． | ∠B、∠C都不是锐角 | B． | ∠B为锐角 | C． | ∠C不为锐角 | D． | ∠B、∠C不都是锐角 |
将一块直角三角板与一两边平行的纸条按如图所示位置放置，若∠1=20°，则∠2=70°．