题目内容
客车和货车同时分别从甲乙两城沿同一公路相向而行，相遇时客车比货车多行驶了180千米，相遇后，客车再经过4小时到达乙城，货车再经过9小时到达甲城，求客车、货车的速度和甲乙两城间的路程．
考点：分式方程的应用
专题：
分析：可设客车的速度是x千米/小时，则货车的速度是
千米/小时，以相遇时时间相等作为等量关系，列出方程求解即可．
| 4x+180 |
| 9 |
解答：解：设客车的速度是x千米/小时，则货车的速度是
千米/小时，依题意有
=
，
解得x1=90，x2=-18（不合题意舍去），
经检验，x=90是原方程的解，
=
=60，
90×4+60×9
=360+540
=900（千米）．
答：客车的速度是90千米/小时，则货车的速度是60千米/小时，甲乙两城间的路程是900千米．
| 4x+180 |
| 9 |
| 4x+180 |
| x |
| 4x | ||
|
解得x1=90，x2=-18（不合题意舍去），
经检验，x=90是原方程的解，
| 4x+180 |
| 9 |
| 4×90+180 |
| 9 |
90×4+60×9
=360+540
=900（千米）．
答：客车的速度是90千米/小时，则货车的速度是60千米/小时，甲乙两城间的路程是900千米．
点评：本题考查分式方程的应用，分析题意，找到合适的等量关系是解决问题的关键．注意分式方程要验根．
练习册系列答案
相关题目
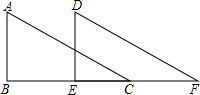如图，Rt△ABC沿直角边BC所在直线向右平移得到△DEF，下列结论：
计算图中阴影部分的面积．
如图，在5×7的方格中，点A、B都在小方格的顶点上，请在图1，图2中各画一个Rt△ABC，要求点C在小正方形的顶点上，且所画的两个三角形不全等．
如图，在正方形铁皮上剪下一个扇形，又在剩余部分剪去一个最大的扇形．用它们能否围成一个圆锥？为什么？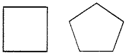
如图，同一段铁丝分成相等的四段可围成正方形，若分成相等的五段，则可围成正五边形，其中正方形的边长为（