题目内容
 如图,同一段铁丝分成相等的四段可围成正方形,若分成相等的五段,则可围成正五边形,其中正方形的边长为(
如图,同一段铁丝分成相等的四段可围成正方形,若分成相等的五段,则可围成正五边形,其中正方形的边长为(| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
考点:配方法的应用,非负数的性质:偶次方
专题:应用题
分析:先根据题意得出4(
a2-
ab+
b2)=5(2b-5),然后进行化简得出4a2-4ab+b2+b2-10b+25=0,再根据配方法的步骤求出a,b的值,再根据正五边形的周长公式即可求出答案.
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:根据题意得:4(
a2-
ab+
b2)=5(2b-5),
整理得:a2-2ab+2b2=10b-25,即a2-2ab+2b2-10b+25=0,
配方得:a2-2ab+b2+b2-10b+25=0,即(a-b)2+(b-5)2=0,
∵(a-b)2≥0,(b-5)2≥0,
∴a-b=0,b-5=0,
∴a=b=5,
∴这段铁丝的总长是5(2b-5)=5×(2×5-5)=25m.
故答案为:25
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
整理得:a2-2ab+2b2=10b-25,即a2-2ab+2b2-10b+25=0,
配方得:a2-2ab+b2+b2-10b+25=0,即(a-b)2+(b-5)2=0,
∵(a-b)2≥0,(b-5)2≥0,
∴a-b=0,b-5=0,
∴a=b=5,
∴这段铁丝的总长是5(2b-5)=5×(2×5-5)=25m.
故答案为:25
点评:此题考查了配方法的应用,解题的关键是根据4(
a2-
ab+
b2)=5(2b-5)得出(2a-b)2+(b-5)2=0.
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |

练习册系列答案
相关题目
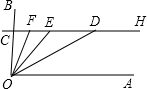 如图,在∠AOB的边OB上取一点C,过点C作CH∥OA,D、E、F在CH上,且满足OD平分∠EOA,OF平分∠COE,∠AOB=88°.
如图,在∠AOB的边OB上取一点C,过点C作CH∥OA,D、E、F在CH上,且满足OD平分∠EOA,OF平分∠COE,∠AOB=88°.