题目内容
5.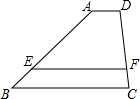 如图,已知AD∥EF∥BC,AE=3BE,AD=2,EF=5,那么BC=$\frac{17}{3}$.
如图,已知AD∥EF∥BC,AE=3BE,AD=2,EF=5,那么BC=$\frac{17}{3}$.
分析 首先延长BA与CD,相交于点G,由AD∥EF∥BC,可得△GAD∽△GEF,△GAD∽△GBC,又由AD=2,EF=5,根据相似三角形的对应边成比例,即可求得BC的长.
解答 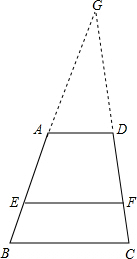 解:延长BA与CD,相交于点G,
解:延长BA与CD,相交于点G,
∵AD∥EF∥BC,
∴△GAD∽△GEF,△GAD∽△GBC,
∴$\frac{AD}{EF}$=$\frac{GA}{GB}$=$\frac{AD}{BC}$,
∵AD=2,EF=,AE=9,
∴$\frac{2}{5}$=$\frac{GA}{GA+9}$,
解得:GA=6,
∴GB=GA+AE+BE=18,
∴$\frac{6}{18}$=$\frac{2}{BC}$,
解得:BC=6.
故答案为:6.
点评 此题考查了相似三角形的判定与性质以及平行线分线段成比例定理.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
相关题目
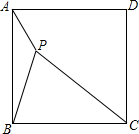 如图,P是正方形ABCD内的一点,PA=1,PB=2,PC=3,
如图,P是正方形ABCD内的一点,PA=1,PB=2,PC=3,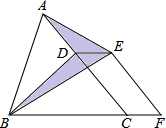 如图,已知△ABC的面积为24,点D在线段AC上,点F在线段BC的延长线上,且BF=4CF,四边形DCFE是平行四边形,则图中阴影部分的面积为( )
如图,已知△ABC的面积为24,点D在线段AC上,点F在线段BC的延长线上,且BF=4CF,四边形DCFE是平行四边形,则图中阴影部分的面积为( )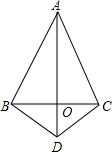 如图,在△ABC中,AB=AC,点O是BC的中点,连接AO,在AO的延长线上取一点D,连接BD,CD
如图,在△ABC中,AB=AC,点O是BC的中点,连接AO,在AO的延长线上取一点D,连接BD,CD