题目内容
11.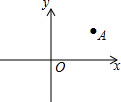 如图,已知点A(2,3),将点A绕原点O顺时针旋转90°到A′,则点A′的坐标为( )
如图,已知点A(2,3),将点A绕原点O顺时针旋转90°到A′,则点A′的坐标为( )| A. | (-2,3) | B. | (-3,2) | C. | (2,-3) | D. | (3,-2) |
分析 作出图形,过点A作AB⊥x轴于B,过点A′作A′B′⊥y轴于B′,然后根据点A的坐标求出AB、OB,再根据旋转的性质求出A′B′,OB′,然后写出点A′的坐标即可.
解答  解:如图,过点A作AB⊥x轴于B,过点A′作A′B′⊥y轴于B′,
解:如图,过点A作AB⊥x轴于B,过点A′作A′B′⊥y轴于B′,
∵A(2,3),
∴AB=3,OB=2,
∵将点A绕原点O顺时针旋转90°到A′,
∴A′B′=AB=3,OB′=OB=2,
∴点A′(3,-2).
故选D.
点评 本题考查了坐标与图形变化-旋转,熟练掌握旋转的性质是解题的关键,作出图形更形象直观.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
13.下列各式中,计算结果为a6的是( )
| A. | a2+a4 | B. | (a2)4 | C. | a2•a3 | D. | a7÷a |
1.若某同学在一次综合性测试中,语文、数学、英语、科学、社会5门学科的名次在其所在班级里都不超过3(记第一名为1,第二名为2,第三名为3,以此类推且没有并列名次情况),则称该同学为超级学霸.现根据不同班级的甲、乙、丙、丁四位同学对一次综合性测试名次数据的描述,一定可以推断是超级学霸的是( )
| A. | 甲同学:平均数为2,中位数为2 | B. | 乙同学:中位数是2,唯一的众数为2 | ||
| C. | 丙同学:平均数是2,标准差为2 | D. | 丁同学:平均数为2,唯一的众数为2 |
 如图,在两条交叉的公路L1与L2之间有两家工厂A、B,现在要修一个货物中转站,使它到两条公路的距离相等,以及到两个工厂距离相等,你能帮助确定中转站的地址吗?请试试.
如图,在两条交叉的公路L1与L2之间有两家工厂A、B,现在要修一个货物中转站,使它到两条公路的距离相等,以及到两个工厂距离相等,你能帮助确定中转站的地址吗?请试试. 如图,已知△ABC的面积为24,点D在线段AC上,点F在线段BC的延长线上,且BF=4CF,四边形DCFE是平行四边形,则图中阴影部分的面积为( )
如图,已知△ABC的面积为24,点D在线段AC上,点F在线段BC的延长线上,且BF=4CF,四边形DCFE是平行四边形,则图中阴影部分的面积为( )