题目内容
6.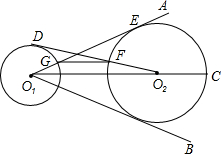 如图,⊙O1与⊙O2外离,O1C是∠AO1B的角平分线,O1C经过点O2,O1A切⊙O2于点E,交⊙O1于点G.
如图,⊙O1与⊙O2外离,O1C是∠AO1B的角平分线,O1C经过点O2,O1A切⊙O2于点E,交⊙O1于点G.(1)求证:O1B是⊙O2的切线;
(2)过O2作⊙O1的切线O2D(D为切点),交⊙O2于点F,判断GF与O1O2的位置关系,并证明你的结论.
分析 (1)连接EO2,作O2M⊥O1B,垂足为M,利用角平分线性质只要证明O2E=O2M即可.
(2)利用相似三角形性质只要证明$\frac{OG}{O{O}_{1}}$=$\frac{OF}{O{O}_{2}}$即可.
解答 (1)证明:连接EO2,作O2M⊥O1B,垂足为M.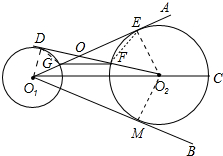 ∵O1A是⊙O2切线,
∵O1A是⊙O2切线,
∴O2E⊥O1A,
∵O1O2平分∠AO1B,
∴O2E=O2M,
∴O1B是⊙O2的切线.
(2)结论:FG∥O1O2,理由如下,
连接O1D,DG,EF,
∵O2D,O1A是切线,
∴O1D⊥OD,O2E⊥OE,
∴∠O1DO=∠O2EO,
∵∠DOG=∠EOF,∠DO1O+∠DOG=90°,∠EO2O+∠EOF=90°,
∴∠DO1O=∠EO2O,
∵∠O1DO=∠O2EO=90°,
∴△O1DO∽△O2EO,
∴$\frac{OD}{O{O}_{1}}$=$\frac{OE}{O{O}_{2}}$,
∴$\frac{DO}{OE}$=$\frac{O{O}_{1}}{O{O}_{2}}$,
∵O1D=O1G,O2E=O2F,
∴∠O1DG=∠O1GD=∠O2EF=∠O2FE,
∴∠GDO=∠FOE,
∴△DOG∽△EOF,
∴$\frac{DO}{OG}$=$\frac{OE}{OF}$,
∴$\frac{DO}{OE}$=$\frac{OG}{OF}$,
∴$\frac{O{O}_{1}}{O{O}_{2}}$=$\frac{OG}{OF}$,
∴$\frac{OG}{O{O}_{1}}$=$\frac{OF}{O{O}_{2}}$,
∴FG∥O1O2.
点评 本题考查切线的判定和性质、相似三角形的判定和性质、平行线的判定、角平分线的性质等知识,解题的关键是正确寻找相似三角形,利用相似三角形的性质解决问题,属于中考常考题型.

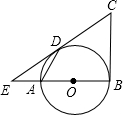 如图,AB为⊙O的直径,CB、CD分别与⊙O相切于B、D,延长BA、CD交于E,连接AD,DE=4,BE=8.
如图,AB为⊙O的直径,CB、CD分别与⊙O相切于B、D,延长BA、CD交于E,连接AD,DE=4,BE=8.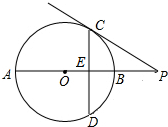 如图,AB是⊙O的直径,P是AB延长线上一点,PC切⊙O于C,作C关于AP的对称点D,连接CD交AB于E,且AB=6,OE=1,则PC=6$\sqrt{2}$.
如图,AB是⊙O的直径,P是AB延长线上一点,PC切⊙O于C,作C关于AP的对称点D,连接CD交AB于E,且AB=6,OE=1,则PC=6$\sqrt{2}$.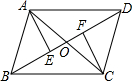 如图,在?ABCD中,AC与BD相交于点O,AE⊥BD于E,AF⊥BD于F,则图中的全等三角形共有6对.
如图,在?ABCD中,AC与BD相交于点O,AE⊥BD于E,AF⊥BD于F,则图中的全等三角形共有6对.