题目内容
5. 如图,在平面直角坐标系xOy中,抛物线y=x2+bx+c与x轴只有一个交点M,与平行于x轴的直线l交于A、B两点,若AB=3,则点M到直线l的距离为( )
如图,在平面直角坐标系xOy中,抛物线y=x2+bx+c与x轴只有一个交点M,与平行于x轴的直线l交于A、B两点,若AB=3,则点M到直线l的距离为( )| A. | $\frac{5}{2}$ | B. | $\frac{9}{4}$ | C. | 2 | D. | $\frac{7}{4}$ |
分析 设M到直线l的距离为m,则有x2+bx+c=m两根的差为3,又x2+bx+c=0时,△=0,列式求解即可.
解答 解:抛物线y=x2+bx+c与x轴只有一个交点,
∴△=b2-4ac=0,
∴b2-4c=0,
设M到直线l的距离为m,则有x2+bx+c=m两根的差为3,
${(x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}={(x}_{1}-{x}_{2})^{2}$
可得:b2-4(c-m)=9,
解得:m=$\frac{9}{4}$.
故答案选B.
点评 此题主要考查抛物线与x轴和直线的交点问题,会用根的判别式和根与系数的关系进行列式求解是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.3-2与32的关系为( )
| A. | 互为相反数 | B. | 互为倒数 | C. | 和为零 | D. | 绝对值相等 |
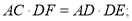
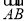 的中点,连接MD交弦AB于点H,若
的中点,连接MD交弦AB于点H,若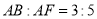 ,证明:
,证明: 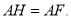
 如图,AB是⊙O的直径,C是AB延长线上的一点,CD切⊙O于点D,且∠ABD=2∠BDC.
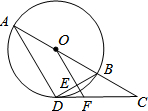
如图,AB是⊙O的直径,C是AB延长线上的一点,CD切⊙O于点D,且∠ABD=2∠BDC.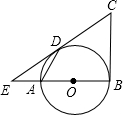 如图,AB为⊙O的直径,CB、CD分别与⊙O相切于B、D,延长BA、CD交于E,连接AD,DE=4,BE=8.
如图,AB为⊙O的直径,CB、CD分别与⊙O相切于B、D,延长BA、CD交于E,连接AD,DE=4,BE=8.