题目内容
9.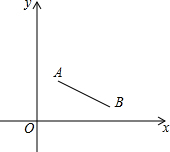 如图,点A、B的坐标分别为(1,2),(3,$\frac{1}{2}$),现将线段AB绕点B顺时针旋转180°得线段A1B,则A1的坐标为( )
如图,点A、B的坐标分别为(1,2),(3,$\frac{1}{2}$),现将线段AB绕点B顺时针旋转180°得线段A1B,则A1的坐标为( )| A. | (1,-5) | B. | (5,-2) | C. | (5,-1) | D. | (-1,5) |
分析 设A1的坐标为(m,n),根据旋转的性质得BA=BA1,∠ABA1=180°,则可判断点B为AA1的中点,根据线段中点坐标公式得到3=$\frac{1+a}{2}$,$\frac{1}{2}$=$\frac{2+b}{2}$,解得a=5,b=-1,然后解方程求出a、b即可得到A1的坐标.
解答 解:设A1的坐标为(m,n),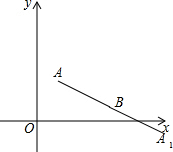
∵线段AB绕点B顺时针旋转180°得线段A1B,
∴BA=BA1,∠ABA1=180°,
∴点B为AA1的中点,
∴3=$\frac{1+a}{2}$,$\frac{1}{2}$=$\frac{2+b}{2}$,解得a=5,b=-1,
∴A1的坐标为(5,-1).
故选C.
点评 本题考查了坐标与图形变化-旋转:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30°,45°,60°,90°,180°.利用线段中点坐标公式是解决本题的关键.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
19.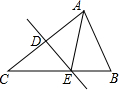 如图,△ABC中,DE垂直平分AC,垂足为D,AD=3,△ABE的周长为13,那么△ABC的周长为( )
如图,△ABC中,DE垂直平分AC,垂足为D,AD=3,△ABE的周长为13,那么△ABC的周长为( )
 如图,△ABC中,DE垂直平分AC,垂足为D,AD=3,△ABE的周长为13,那么△ABC的周长为( )
如图,△ABC中,DE垂直平分AC,垂足为D,AD=3,△ABE的周长为13,那么△ABC的周长为( )| A. | 10 | B. | 13 | C. | 16 | D. | 19 |
4.下列方程为一元二次方程的是( )
| A. | x+$\frac{1}{x}$=1 | B. | ax2+bx+c=0 | C. | x(x-1)=x | D. | x+$\sqrt{x-1}=0$ |
1.方程|$\frac{x-1}{2}$|+|$\frac{1-x}{3}$|=0的解是( )
| A. | 1 | B. | 无数个 | C. | 0 | D. | 无解 |
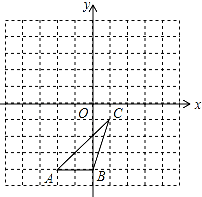 如图,△ABC各顶点的坐标分别是A(-2,-4),B(0,-4),C(1,-1)
如图,△ABC各顶点的坐标分别是A(-2,-4),B(0,-4),C(1,-1)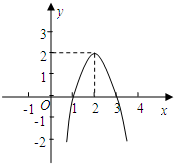 二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象回答:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象回答: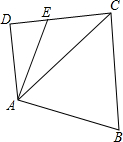 如图,E是四边形ABCD的DC边上一点,CE=$\sqrt{2}$,AB=2,BC=$\sqrt{3}+1$,∠D=90°,∠B=60°,S四边形ABCE=$\frac{3+2\sqrt{3}}{2}$
如图,E是四边形ABCD的DC边上一点,CE=$\sqrt{2}$,AB=2,BC=$\sqrt{3}+1$,∠D=90°,∠B=60°,S四边形ABCE=$\frac{3+2\sqrt{3}}{2}$