题目内容
10.已知二次函数y=ax2+bx+c(a>0)与一次函数y=kx+m的图象相交于A(-2,1)、B(3,6)两点,则能使关于x的不等式ax2+bx+c<kx+m成立的x的取值范围是-2<x<3.分析 根据题意在同一坐标系内画出函数的图象,利用数形结合即可得出结论.
解答  解:如图所示,
解:如图所示,
由图可知,关于x的不等式ax2+bx+c<kx+m成立的x的取值范是:-2<x<3.
故答案为:-2<x<3.
点评 本题考查的是二次函数与不等式,能根据题意画出图形,利用数形结合求解是解答此题的关键.

练习册系列答案
相关题目
1.方程|$\frac{x-1}{2}$|+|$\frac{1-x}{3}$|=0的解是( )
| A. | 1 | B. | 无数个 | C. | 0 | D. | 无解 |
5.二次函数y=kx2-6x+3的图象与x轴有交点,则k的取值范围是( )
| A. | k≤3且k≠0 | B. | k<3且k≠0 | C. | k≤3 | D. | k<3 |
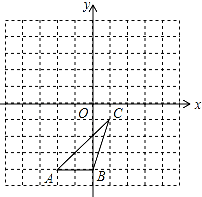 如图,△ABC各顶点的坐标分别是A(-2,-4),B(0,-4),C(1,-1)
如图,△ABC各顶点的坐标分别是A(-2,-4),B(0,-4),C(1,-1)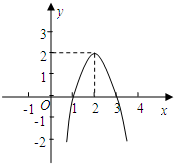 二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象回答:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象回答: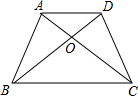 如图,四边形ABCD,AD∥BC,对角线AC,BD相交于点O,△AOD和△ABO的面积分别为2cm2和3cm2,求四边形ABCD的面积.
如图,四边形ABCD,AD∥BC,对角线AC,BD相交于点O,△AOD和△ABO的面积分别为2cm2和3cm2,求四边形ABCD的面积.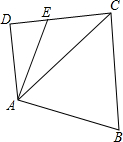 如图,E是四边形ABCD的DC边上一点,CE=$\sqrt{2}$,AB=2,BC=$\sqrt{3}+1$,∠D=90°,∠B=60°,S四边形ABCE=$\frac{3+2\sqrt{3}}{2}$
如图,E是四边形ABCD的DC边上一点,CE=$\sqrt{2}$,AB=2,BC=$\sqrt{3}+1$,∠D=90°,∠B=60°,S四边形ABCE=$\frac{3+2\sqrt{3}}{2}$