题目内容
16.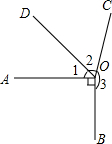 (1)从点O引四条射线OA,OB,OC,OD,如果∠AOB:∠BOC:∠COD:∠DOA=1:2:3:4,那么这四个角的度数分别是多少?
(1)从点O引四条射线OA,OB,OC,OD,如果∠AOB:∠BOC:∠COD:∠DOA=1:2:3:4,那么这四个角的度数分别是多少?(2)如图所示,∠AOB=90°,OD平分∠AOC,∠3=3∠1,求∠2的度数.
分析 (1)根据已知得出∠AOD+∠AOB+∠BOC+∠COD=360°,设∠AOB=x°,∠BOC=2x°,∠COD=3x°,∠OAD=4x°,得出方程x+2x+3x+4x=360,求出即可;
(2)根据角平分线的定义得到∠1=∠2,等量代换得到∠3=3∠2,根据周角的定义列方程即可得到结论.
解答 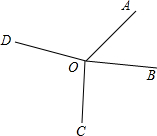 解:(1)∵∠AOB:∠BOC:∠COD:∠DOA=1:2:3:4,
解:(1)∵∠AOB:∠BOC:∠COD:∠DOA=1:2:3:4,
∴∠AOD≠∠AOB+∠BOC+∠COD,
即∠AOD+∠AOB+∠BOC+∠COD=360°,
设∠AOB=x°,∠BOC=2x°,∠COD=3x°,∠AOD=4x°,
则x+2x+3x+4x=360,
x=36,
∴∠AOB=36°,∠BOC=72°,∠COD=108°,∠AOD=144°;
(2)∵OD平分∠AOC,
∴∠1=∠2,
∵∠3=3∠1,
∴∠3=3∠2,
∵∠1+∠2+∠3+∠AOB=360°,
即∠2+∠2+3∠2+90°=360°,
∴∠2=54°.
点评 本题考查了本题考查了角的计算,角平分线的定义,解此题的关键是根据周角的定义得出的方程.

练习册系列答案
相关题目
4.下列方程为一元二次方程的是( )
| A. | x+$\frac{1}{x}$=1 | B. | ax2+bx+c=0 | C. | x(x-1)=x | D. | x+$\sqrt{x-1}=0$ |
1.方程|$\frac{x-1}{2}$|+|$\frac{1-x}{3}$|=0的解是( )
| A. | 1 | B. | 无数个 | C. | 0 | D. | 无解 |
5.二次函数y=kx2-6x+3的图象与x轴有交点,则k的取值范围是( )
| A. | k≤3且k≠0 | B. | k<3且k≠0 | C. | k≤3 | D. | k<3 |
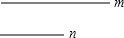 ①已知线段m和n,请用直尺和圆规作出等腰△ABC,使得AB=AC,BC=m,∠A的平分线等于n.(只保留作图痕迹,不写作法)
①已知线段m和n,请用直尺和圆规作出等腰△ABC,使得AB=AC,BC=m,∠A的平分线等于n.(只保留作图痕迹,不写作法)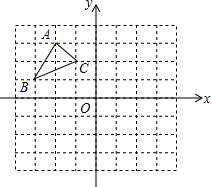 如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度;已知△ABC.
如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度;已知△ABC. 如果一个点与另外两个点能构成直角三角形,则称这个点为另外两个点的勾股点.例如:矩形ABCD中,点C与A、B两点可构成直角三角形ABC,则称点C为A、B两点的勾股点,同样,点D也是A、B两点的勾股点.
如果一个点与另外两个点能构成直角三角形,则称这个点为另外两个点的勾股点.例如:矩形ABCD中,点C与A、B两点可构成直角三角形ABC,则称点C为A、B两点的勾股点,同样,点D也是A、B两点的勾股点.