��Ŀ����
4��С����һЩ��ͬ�������壨����������������4cm2��Сľ���������ϴ�ģ���ݣ�С����һ��������������ʱ������ij���Ƭ����ͼ��ʾ��������С��������С��д���������������⣬�����С����ɣ�����һ���Ҵ����������ʱ������������Сľ��¶������ı��������������������ӵIJ��֣����ܺ��Ƕ��٣�
��������һ�������Ƭ�еĹ��ɴ���ȥ�����Ҵ��n������ʱ�������������������Сľ��¶������ı��������������������ӵIJ��֣����ܺͣ���ʾ��1+2+3+��+n=$\frac{n��n+1��}{2}$���ú�n�Ĵ���ʽ��ʾ��
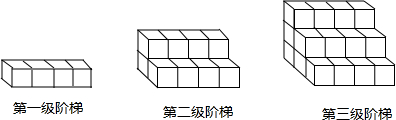
���� ��1����������������ʱ������������Сľ��¶������ı�������㼴�ɣ�
��2�������һ�㣬���ݣ�1���ҵ���ʾ����������Сľ��¶������������θ�����ͨʽ���ɣ�
��� �⣺��1�������������ʱ������������Сľ��¶������������θ�����4��3��3+2��1+2+3��=48��������������Сľ��¶������ı����Ϊ��48��4=192��cm2����
��2�����n������ʱ������������Сľ��¶������������θ�����4��3��n+2��1+2+3+��+n��=12n+n��n+1��=n2+13n������������Сľ��¶������ı����Ϊ����n2+13n����4=4n2+52n��cm2����
���� ������Ҫ����ѧ����ͼ�α仯���������������գ���������Ŀ�Ĺؼ��Ǹ�����Ŀ�и�����ͼ�Ρ���ֵ�����ݵ�����������������ҵ����ɣ�������Ŀ�Ѷ����У������е��⣮

��ϰ��ϵ�д�
 ÿ��10���ӿ�����������������ϵ�д�
ÿ��10���ӿ�����������������ϵ�д�
�����Ŀ
16��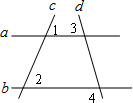 ��ͼ��ֱ��a��b��ֱ��c��d�ཻ������1=��2����3=70�㣬��4�Ķ���Ϊ��������
��ͼ��ֱ��a��b��ֱ��c��d�ཻ������1=��2����3=70�㣬��4�Ķ���Ϊ��������
 ��ͼ��ֱ��a��b��ֱ��c��d�ཻ������1=��2����3=70�㣬��4�Ķ���Ϊ��������
��ͼ��ֱ��a��b��ֱ��c��d�ཻ������1=��2����3=70�㣬��4�Ķ���Ϊ��������| A�� | 35�� | B�� | 70�� | C�� | 90�� | D�� | 110�� |
13��������x��һԪ���η���x2+ax+b=0��������ͬ��ʵ����m��n��m��n��������x2+ax+b=2��������ͬ��ʵ����p��q��p��q������m��n��p��q�Ĵ�С��ϵΪ��������
| A�� | p��m��n��q | B�� | m��p��q��n | C�� | m��p��n��q | D�� | p��m��q��n |
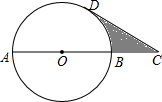 ��ͼ��ABΪ��O��ֱ������C��AB���ӳ����ϣ���AB=2BC=4��CD���O�����ڵ�D����ͼ����Ӱ���ֵ������2$\sqrt{3}$-$\frac{2}{3}$�У�������������źͦУ�
��ͼ��ABΪ��O��ֱ������C��AB���ӳ����ϣ���AB=2BC=4��CD���O�����ڵ�D����ͼ����Ӱ���ֵ������2$\sqrt{3}$-$\frac{2}{3}$�У�������������źͦУ�