题目内容
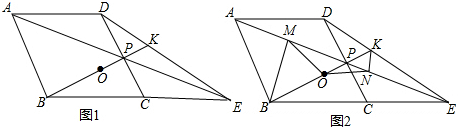
11.如图,菱形ABCD中,点P是CD的中点,∠BCD=60°,射线AP交BC的延长线于点E,射线BP交DE于点K,点O是线段BK的中点.(1)求证:△ADP≌△ECP;
(2)若BP=n•PK,试求出n的值;
(3)作BM丄AE于点M,作KN丄AE于点N,连结MO、NO,如图2所示,请证明△MON是等腰三角形,并直接写出∠MON的度数.
分析 (1)根据菱形的性质得到AD∥BC,根据平行线的性质得到对应角相等,根据全等三角形的判定定理证明结论;
(2)作PI∥CE交DE于I,根据点P是CD的中点证明CE=2PI,BE=4PI,根据相似三角形的性质证明结论;
(3)作OG⊥AE于G,根据平行线等分线段定理得到MG=NG,又OG⊥MN,证明△MON是等腰三角形,根据直角三角形的性质和锐角三角函数求出∠MON的度数.
解答 (1)证明:∵四边形ABCD为菱形,
∴AD∥BC,
∴∠DAP=∠CEP,∠ADP=∠ECP,
在△ADP和△ECP中,
$\left\{\begin{array}{l}{∠DAP=∠CEP}\\{∠ADP=∠ECP}\\{DP=CP}\end{array}\right.$,
∴△ADP≌△ECP;
(2)如图1,作PI∥CE交DE于I,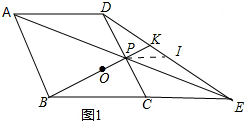
则$\frac{PI}{CE}$=$\frac{DP}{DC}$,又点P是CD的中点,
∴$\frac{PI}{CE}$=$\frac{1}{2}$,
∵△ADP≌△ECP,
∴AD=CE,
∴$\frac{KP}{KB}$=$\frac{PI}{BE}$=$\frac{1}{4}$,
∴BP=3PK,
∴n=3;
(3)如图2,作OG⊥AE于G,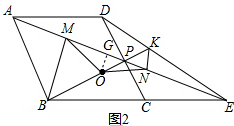
∵BM丄AE于M,KN丄AE于N,
∴BM∥OG∥KN,
∵点O是线段BK的中点,
∴MG=NG,又OG⊥MN,
∴OM=ON,
即△MON是等腰三角形,
由题意得,△BPC,△AMB,△ABP为直角三角形,
设BC=2,则CP=1,由勾股定理得,BP=$\sqrt{3}$,
则AP=$\sqrt{7}$,
根据三角形面积公式,BM=$\frac{2\sqrt{21}}{7}$,
由(2)得,PB=3PO,
∴OG=$\frac{1}{3}$BM=$\frac{2\sqrt{21}}{21}$,
MG=$\frac{2}{3}$MP=$\frac{2}{7}\sqrt{7}$,
tan∠MOG=$\frac{MG}{OG}$=$\sqrt{3}$,
∴∠MOG=60°,
∴∠MON的度数为120°.
点评 本题考查的是菱形的性质和相似三角形的判定和性质、全等三角形的判定和性质,灵活运用判定定理和性质定理是解题的关键,注意锐角三角函数在解题中的运用.

| A. | y=(x-1)2+2 | B. | y=(x+1)2+2 | C. | y=(x-1)2-2 | D. | y=(x+1)2-2 |
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
①b=-4;
②存在这样一个a,使得M、A、C三点在同一条直线上;
③抛物线的对称轴位于y轴的右侧;
④若a=1,则3OA•OB=OC2.
正确的有( )
| A. | ①②③ | B. | ①②④ | C. | ②③④ | D. | ①③④ |
| A. | y1+y2>0 | B. | y1-y2>0 | C. | a(y1-y2)>0 | D. | a(y1+y2)>0 |
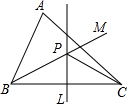 如图,锐角三角形ABC中,直线PL为BC的垂直平分线,射线BM为∠ABC的平分线,PL与BM相交于P点.若∠PBC=30°,∠ACP=20°,则∠A的度数为70°.
如图,锐角三角形ABC中,直线PL为BC的垂直平分线,射线BM为∠ABC的平分线,PL与BM相交于P点.若∠PBC=30°,∠ACP=20°,则∠A的度数为70°.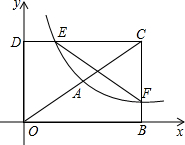 如图,在平面直角坐标系xOy中,已知四边形DOBC是矩形,且D(O,4),B(6,0).若反比例函数y=$\frac{{k}_{1}}{x}$(x>0)的图象经过线段OC的中点A,分别交DC于点E,交BC于点F.设直线EF的解析式为y=k2x+b
如图,在平面直角坐标系xOy中,已知四边形DOBC是矩形,且D(O,4),B(6,0).若反比例函数y=$\frac{{k}_{1}}{x}$(x>0)的图象经过线段OC的中点A,分别交DC于点E,交BC于点F.设直线EF的解析式为y=k2x+b