题目内容
9.观察探究及应用(1)观察图并填空
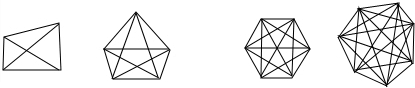
一个四边形有2条对角线
一个五边形有5条对角线
一个六边形有9对角线
一个七边形有14对角线
(2)分析探究:由凸n边形的一个顶点出发,可做(n-3)对角线,若允许重复计数,共可作n(n-3)条对角线;
(3)结论:一个凸n边形有$\frac{n(n-3)}{2}$条对角线;
(4)应用:一个凸十二边形有54对角线.
分析 (1)根据图形数出对角线条数即可;
(2)根据n边形从一个顶点出发可引出(n-3)条对角线即可求解;
(3)由(2)可知,任意凸n边形的对角线有条$\frac{n(n-3)}{2}$,即可解答;
(4)由(3)把n=12代入计算即可.
解答 解:(1)根据图形数出对角线条数,一个四边形有2条对角线,一个五边形有5条对角线,一个六边形有9对角线,一个七边形有14对角线;
故答案为:9;14.
(2)n边形从一个顶点出发可引出(n-3)条对角线,若允许重复计数,共可作n(n-3)条对角线;
故答案为:(n-3);n(n-3).
(3)由(2)可知,任意凸n边形的对角线有条$\frac{n(n-3)}{2}$,故答案为:$\frac{n(n-3)}{2}$.
(4)把n=12代入$\frac{n(n-3)}{2}$计算得:$\frac{12×9}{2}$=54.
故答案为:54.
点评 本题考查了多边形的对角线,解题关键是n边形从一个顶点出发的对角线有(n-3)条.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.下列分式一定有意义的是( )
| A. | $\frac{{x}^{2}+1}{{x}^{2}-1}$ | B. | $\frac{x+1}{x^2}$ | C. | $\frac{x-1}{{x}^{2}+1}$ | D. | $\frac{{x}^{2}}{x+1}$ |
18.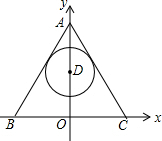 如图,△ABC是边长为6的等边三角形,以BC所在直线为x轴,BC的垂直平分线为y轴建立平面直角坐标系,点D为射线AO上任意一点(不与点A重合),以点D为圆心的圆始终与AB所在直线相切,在点D沿着射线AO平移的过程中,⊙D与x轴相切时,其半径为( )
如图,△ABC是边长为6的等边三角形,以BC所在直线为x轴,BC的垂直平分线为y轴建立平面直角坐标系,点D为射线AO上任意一点(不与点A重合),以点D为圆心的圆始终与AB所在直线相切,在点D沿着射线AO平移的过程中,⊙D与x轴相切时,其半径为( )
 如图,△ABC是边长为6的等边三角形,以BC所在直线为x轴,BC的垂直平分线为y轴建立平面直角坐标系,点D为射线AO上任意一点(不与点A重合),以点D为圆心的圆始终与AB所在直线相切,在点D沿着射线AO平移的过程中,⊙D与x轴相切时,其半径为( )
如图,△ABC是边长为6的等边三角形,以BC所在直线为x轴,BC的垂直平分线为y轴建立平面直角坐标系,点D为射线AO上任意一点(不与点A重合),以点D为圆心的圆始终与AB所在直线相切,在点D沿着射线AO平移的过程中,⊙D与x轴相切时,其半径为( )| A. | $\sqrt{3}$ | B. | 3 | C. | $\sqrt{3}$或3$\sqrt{3}$ | D. | 2$\sqrt{3}$或3$\sqrt{3}$ |
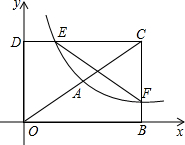 如图,在平面直角坐标系xOy中,已知四边形DOBC是矩形,且D(O,4),B(6,0).若反比例函数y=$\frac{{k}_{1}}{x}$(x>0)的图象经过线段OC的中点A,分别交DC于点E,交BC于点F.设直线EF的解析式为y=k2x+b
如图,在平面直角坐标系xOy中,已知四边形DOBC是矩形,且D(O,4),B(6,0).若反比例函数y=$\frac{{k}_{1}}{x}$(x>0)的图象经过线段OC的中点A,分别交DC于点E,交BC于点F.设直线EF的解析式为y=k2x+b
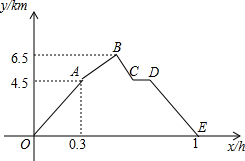 从甲地到乙地,先是一段平路,然后是一段上坡路,小明骑车从甲地出发,到达乙地后立即返回甲地,途中休息了一段时间,假设小明骑车在平路、上坡、下坡时分别保持匀速前进,已知小明骑车上坡的速度比在平路上的速度每小时少5km.下坡的速度比在平路上的速度每小时多5km.设小明出发xh后,到达离甲地ykm的方,图中的折线OABCDE 表示y与x之间的函数关系,有下列说法正确的有( )个
从甲地到乙地,先是一段平路,然后是一段上坡路,小明骑车从甲地出发,到达乙地后立即返回甲地,途中休息了一段时间,假设小明骑车在平路、上坡、下坡时分别保持匀速前进,已知小明骑车上坡的速度比在平路上的速度每小时少5km.下坡的速度比在平路上的速度每小时多5km.设小明出发xh后,到达离甲地ykm的方,图中的折线OABCDE 表示y与x之间的函数关系,有下列说法正确的有( )个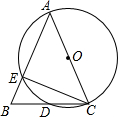 如图,在△ABC中,AB=AC=13,BC=10,以AC为直径画⊙O交BC于点D,交AB于点E,连接CE.
如图,在△ABC中,AB=AC=13,BC=10,以AC为直径画⊙O交BC于点D,交AB于点E,连接CE.