若矩形ABCD的两邻边长分别为一元二次方程x2-7x+12=0的两个实数根.则矩形ABCD的对角线长为5．题目和参考答案——青夏教育精英家教网—

题目内容

9．若矩形ABCD的两邻边长分别为一元二次方程x²-7x+12=0的两个实数根，则矩形ABCD的对角线长为5．

分析首先解方程求得方程的两个根，即可求得矩形的两边长，然后利用勾股定理即可求得对角线长．

解答解：方程x²-7x+12=0，即（x-3）（x-4）=0，
则x-3=0，x-4=0，
解得：x₁=3，x₂=4．
则矩形ABCD的对角线长是：$\sqrt{{3}^{2}+{4}^{2}}$=5．
故答案是：5．

点评本题考查了一元二次方程的解法以及矩形的性质，正确解方程求得矩形的边长是关键．解一元二次方程的基本思想是降次．

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

20．已知二次函数y=a（x-2）²+c，当x=x₁时，函数值为y₁；当x=x₂时，函数值为y₂，若|x₁-2|＞|x₂-2|，则下列表达式正确的是（　　）

y₁+y₂＞0

y₁-y₂＞0

17．方程组$\left\{\begin{array}{l}{（x+1）^{2}+（y-5）^{2}=27}\\{x+y=1}\end{array}\right.$的解为$\left\{\begin{array}{l}{{x}_{1}=\frac{-5+3\sqrt{5}}{2}}\\{{y}_{1}=\frac{7-3\sqrt{5}}{2}}\end{array}\right.$，$\left\{\begin{array}{l}{{x}_{2}=\frac{-5-3\sqrt{5}}{2}}\\{{y}_{2}=\frac{7+3\sqrt{5}}{2}}\end{array}\right.$．

4．

如图，在△ABC中，∠B=40°，∠C=30°，延长BA至点D，则∠CAD的大小为（　　）

14．已知关于x的方程3a-x=$\frac{x}{2}$+3的解为2，则代数式a²-2a+1的值是1．

4．小宇用一些相同的正方体（其六个面的面积都是4cm²）小木块在桌子上搭模型梯，小宇将搭到第一、二、三级阶梯时的情况拍成照片（如图所示）发给了小东，并给小东写出了下面两个问题，请你帮小东完成．
问题一：我搭到第三级阶梯时，所有正方体小木块露在外面的表面积（不包括与桌子相接的部分）的总和是多少？
问题二：我会照着照片中的规律搭下去，当我搭到第n级阶梯时，请你求出所有正方体小木块露在外面的表面积（不包括与桌子相接的部分）的总和（提示：1+2+3+…+n=$\frac{n（n+1）}{2}$，用含n的代数式表示）

1．

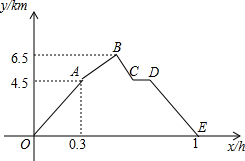从甲地到乙地，先是一段平路，然后是一段上坡路，小明骑车从甲地出发，到达乙地后立即返回甲地，途中休息了一段时间，假设小明骑车在平路、上坡、下坡时分别保持匀速前进，已知小明骑车上坡的速度比在平路上的速度每小时少5km．下坡的速度比在平路上的速度每小时多5km．设小明出发xh后，到达离甲地ykm的方，图中的折线OABCDE 表示y与x之间的函数关系，有下列说法正确的有（　　）个
①小明骑车在平路上的速度为15km/h；
②小明途中休息了0.1h；
③如果小明两次经过途中某一地点的时间间隔为0.15h，那么该地点离甲地5.75km．

2．下列图形既是轴对称图形，又是中心对称图形的是（　　）

试题分类