题目内容
16.若函数y=-kx+2k+2与y=$\frac{k}{x}$(k≠0)的图象有两个不同的交点,则k的取值范围是k>-$\frac{1}{2}$且k≠0.分析 根据反比例函数与一次函数的交点问题,两函数的交点坐标满足方程组$\left\{\begin{array}{l}{y=-kx+2k+2}\\{y=\frac{k}{x}}\end{array}\right.$,接着消去y得到关于x的一元二次方程kx2-(2k+2)x+k=0,由于有两个不同的交点,则关于x的一元二次方程kx2+2x+1=0有两个不相等的实数解,于是根据根的判别式的意义得到△=(2k+2)2-4k2>0,然后解一元一次不等式即可.
解答 解:把方程组$\left\{\begin{array}{l}{y=-kx+2k+2}\\{y=\frac{k}{x}}\end{array}\right.$消去y得到-kx+2k+2=$\frac{k}{x}$,
整理得kx2-(2k+2)x+k=0,
根据题意得△=(2k+2)2-4k2>0,解得k>-$\frac{1}{2}$,
即当k$>-\frac{1}{2}$时,函数y=-kx+2k+2与y=$\frac{k}{x}$(k≠0)的图象有两个不同的交点,
故答案为k$>-\frac{1}{2}$且k≠0.
点评 本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.如果a的倒数是-2,那么a等于( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
4. 如图,在△ABC中,∠B=40°,∠C=30°,延长BA至点D,则∠CAD的大小为( )
如图,在△ABC中,∠B=40°,∠C=30°,延长BA至点D,则∠CAD的大小为( )
 如图,在△ABC中,∠B=40°,∠C=30°,延长BA至点D,则∠CAD的大小为( )
如图,在△ABC中,∠B=40°,∠C=30°,延长BA至点D,则∠CAD的大小为( )| A. | 110° | B. | 80° | C. | 70° | D. | 60° |
11. 某校学生会决定从三名学生会干事中选拔一名干事,对甲、乙、丙三名候选人进行了笔试和面试,三人的测试成绩如下表所示:
某校学生会决定从三名学生会干事中选拔一名干事,对甲、乙、丙三名候选人进行了笔试和面试,三人的测试成绩如下表所示:
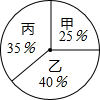
根据录用程序,学校组织200名学生采用投票推荐的方式,对三人进行民主测评,三人得票率(没有弃权,每位同学只能推荐1人)如扇形统计图所示,每得一票记1分.
(1)分别计算三人民主评议的得分;
(2)根据实际需要,学校将笔试、面试、民主评议三项得分按4:3:3的比例确定个人成绩,三人中谁的得分最高?
 某校学生会决定从三名学生会干事中选拔一名干事,对甲、乙、丙三名候选人进行了笔试和面试,三人的测试成绩如下表所示:
某校学生会决定从三名学生会干事中选拔一名干事,对甲、乙、丙三名候选人进行了笔试和面试,三人的测试成绩如下表所示:| 测试项目 | 测试成绩/分 | ||
| 甲 | 乙 | 丙 | |
| 笔试 | 75 | 80 | 90 |
| 面试 | 93 | 70 | 68 |
(1)分别计算三人民主评议的得分;
(2)根据实际需要,学校将笔试、面试、民主评议三项得分按4:3:3的比例确定个人成绩,三人中谁的得分最高?
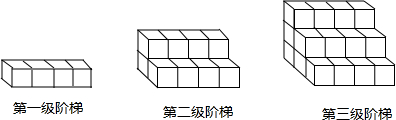
11.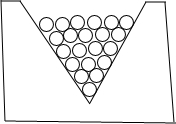 如图所示是工厂里一种统计圆柱形产品(如铅笔)的计数器,工人师傅只要数一数最上层有多少支,就能很快算出产品的总数.
如图所示是工厂里一种统计圆柱形产品(如铅笔)的计数器,工人师傅只要数一数最上层有多少支,就能很快算出产品的总数.
(1)请观察计数器模型,填写下表:
(2)当计数器模型中总共放置了325支产品时,最上层有多少支?
 如图所示是工厂里一种统计圆柱形产品(如铅笔)的计数器,工人师傅只要数一数最上层有多少支,就能很快算出产品的总数.
如图所示是工厂里一种统计圆柱形产品(如铅笔)的计数器,工人师傅只要数一数最上层有多少支,就能很快算出产品的总数.(1)请观察计数器模型,填写下表:
| 最上层的产品数(支) | 1 | 2 | 3 | 4 | … | 10 | … |
| 产品总数 | 1 | 3 | 6 | 10 | … | 55 | … |