题目内容
 如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(-4,6),双曲线y=
如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(-4,6),双曲线y=| k |
| x |
(1)求反比例函数解析式和E点坐标;
(2)若F是OC上一点,且以∠OAF和∠CFD为对应角的△FDC、△AFO相似,求F点的坐标.
考点:反比例函数综合题,坐标与图形性质,相似三角形的性质
专题:综合题
分析:(1)由ABCD为矩形,D为BC中点,根据B坐标确定出D坐标,代入反比例解析式求出中k的值,确定出反比例解析式,将x=-4代入反比例解析式求出y的值,确定出E坐标即可;
(2)如图所示,设F(0,y),根据以∠OAF和∠CFD为对应角的△FDC、△AFO相似,列出比例式,求出y的值,即可确定出F坐标.
(2)如图所示,设F(0,y),根据以∠OAF和∠CFD为对应角的△FDC、△AFO相似,列出比例式,求出y的值,即可确定出F坐标.
解答: 解:(1)∵四边形ABCD为矩形,D为BC中点,B(-4,6),
解:(1)∵四边形ABCD为矩形,D为BC中点,B(-4,6),
∴D(-2,6),
设反比例函数解析式为y=
,
将D(-2,6)代入得:k=-12,
∴反比例解析式为y=-
,
将x=-4代入反比例解析式得:y=3,
则E(-4,3);
(2)设F(0,y),如图所示,连接DF,AF,
∵∠OAF=∠DFC,△AOF∽△FCD,
∴
=
,即
=
,
整理得:y2-6y+8=0,即(y-2)(y-4)=0,
解得:y1=2,y2=4,
则F坐标为(0,2)或(0,4).
 解:(1)∵四边形ABCD为矩形,D为BC中点,B(-4,6),
解:(1)∵四边形ABCD为矩形,D为BC中点,B(-4,6),∴D(-2,6),
设反比例函数解析式为y=
| k |
| x |
将D(-2,6)代入得:k=-12,
∴反比例解析式为y=-
| 12 |
| x |
将x=-4代入反比例解析式得:y=3,
则E(-4,3);
(2)设F(0,y),如图所示,连接DF,AF,
∵∠OAF=∠DFC,△AOF∽△FCD,
∴
| OF |
| OA |
| CD |
| CF |
| y |
| 4 |
| 2 |
| 6-y |
整理得:y2-6y+8=0,即(y-2)(y-4)=0,
解得:y1=2,y2=4,
则F坐标为(0,2)或(0,4).
点评:此题属于反比例函数综合题,涉及的知识有:坐标与图形性质,待定系数法确定函数解析式,相似三角形的性质,以及一元二次方程的解法,熟练掌握待定系数法是解本题的关键.

练习册系列答案
相关题目
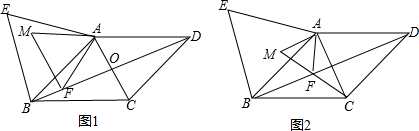
 如图,已知:△OBC为等腰三角形,AB=DC,∠1=∠2.
如图,已知:△OBC为等腰三角形,AB=DC,∠1=∠2. 如图,在平面直角坐标系中,直线l与x轴相交于点M,与y轴相交于点N,Rt△MON的外心为点A(
如图,在平面直角坐标系中,直线l与x轴相交于点M,与y轴相交于点N,Rt△MON的外心为点A( 如图,AB是⊙O的直径,AB=15,AC=9,则tan∠ADC=
如图,AB是⊙O的直径,AB=15,AC=9,则tan∠ADC=