题目内容
如图1,在菱形ABCD中,对角线AC与BD相交于点O,AB=13,BD=24,在菱形ABCD的外部以AB为边作等边三角形 ABE.点F是对角线BD上一动点(点F不与点B重合),将线段AF绕点A顺时针方向旋转60°得到线段AM,连接FM.
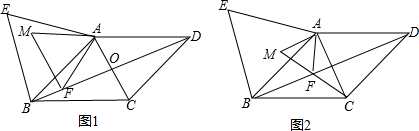
(1)求AO的长;
(2)如图2,当点F在线段BO上,且点M,F,C三点在同一条直线上时,求证:AC=
AM;
(3)连接EM,若△AEM的面积为40,请直接写出△AFM的周长.

(1)求AO的长;
(2)如图2,当点F在线段BO上,且点M,F,C三点在同一条直线上时,求证:AC=
| 3 |
(3)连接EM,若△AEM的面积为40,请直接写出△AFM的周长.
考点:四边形综合题,等边三角形的性质,菱形的性质
专题:几何综合题,压轴题
分析:(1)在RT△OAB中,利用勾股定理OA=
求解,
(2)由四边形ABCD是菱形,求出△AFM为等边三角形,∠M=∠AFM=60°,再求出∠MAC=90°,在Rt△ACM中tan∠M=
,求出AC.
(3)求出△AEM≌△ABF,利用△AEM的面积为40求出BF,在利用勾股定理AF=
=
=
,得出△AFM的周长为3
.
| AB2-OB2 |
(2)由四边形ABCD是菱形,求出△AFM为等边三角形,∠M=∠AFM=60°,再求出∠MAC=90°,在Rt△ACM中tan∠M=
| AC |
| AM |
(3)求出△AEM≌△ABF,利用△AEM的面积为40求出BF,在利用勾股定理AF=
| AO2+FO2 |
| 52+42 |
| 41 |
| 41 |
解答:解:(1)∵四边形ABCD是菱形,
∴AC⊥BD,OB=OD=
BD,
∵BD=24,
∴OB=12,
在Rt△OAB中,
∵AB=13,
∴OA=
=
=5.
(2)如图2,

∵四边形ABCD是菱形,
∴BD垂直平分AC,
∴FA=FC,∠FAC=∠FCA,
由已知AF=AM,∠MAF=60°,
∴△AFM为等边三角形,
∴∠M=∠AFM=60°,
∵点M,F,C三点在同一条直线上,
∴∠FAC+∠FCA=∠AFM=60°,
∴∠FAC=∠FCA=30°,
∴∠MAC=∠MAF+∠FAC=60°+30°=90°,
在Rt△ACM中
∵tan∠M=
,
∴tan60°=
,
∴AC=
AM.
(3)如图,连接EM,

∵△ABE是等边三角形,
∴AE=AB,∠EAB=60°,
由(2)知△AFM为等边三角形,
∴AM=AF,∠MAF=60°,
∴∠EAM=∠BAF,
在△AEM和△ABF中,
,
∴△AEM≌△ABF(SAS),
∵△AEM的面积为40,△ABF的高为AO
∴
BF•AO=40,BF=16,
∴FO=BF-BO=16-12=4
AF=
=
=
,
∴△AFM的周长为3
.
∴AC⊥BD,OB=OD=
| 1 |
| 2 |
∵BD=24,
∴OB=12,
在Rt△OAB中,
∵AB=13,
∴OA=
| AB2-OB2 |
| 132-122 |
(2)如图2,

∵四边形ABCD是菱形,
∴BD垂直平分AC,
∴FA=FC,∠FAC=∠FCA,
由已知AF=AM,∠MAF=60°,
∴△AFM为等边三角形,
∴∠M=∠AFM=60°,
∵点M,F,C三点在同一条直线上,
∴∠FAC+∠FCA=∠AFM=60°,
∴∠FAC=∠FCA=30°,
∴∠MAC=∠MAF+∠FAC=60°+30°=90°,
在Rt△ACM中
∵tan∠M=
| AC |
| AM |
∴tan60°=
| AC |
| AM |
∴AC=
| 3 |
(3)如图,连接EM,

∵△ABE是等边三角形,
∴AE=AB,∠EAB=60°,
由(2)知△AFM为等边三角形,
∴AM=AF,∠MAF=60°,
∴∠EAM=∠BAF,
在△AEM和△ABF中,
|
∴△AEM≌△ABF(SAS),
∵△AEM的面积为40,△ABF的高为AO
∴
| 1 |
| 2 |
∴FO=BF-BO=16-12=4
AF=
| AO2+FO2 |
| 52+42 |
| 41 |
∴△AFM的周长为3
| 41 |
点评:本题主要考查四边形的综合题,解题的关键是灵活运用等边三角形的性质及菱形的性质.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
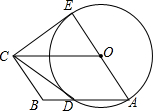 如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于点D,延长AO交⊙O于点E,连接CD,CE,若CE是⊙O的切线,解答下列问题:
如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于点D,延长AO交⊙O于点E,连接CD,CE,若CE是⊙O的切线,解答下列问题: 如图,在平面直角坐标系中,⊙P经过x轴上一点C,与y轴分别相交于A、B两点,连接AP并延长分别交⊙P、x轴于点D、点E,连接DC并延长交y轴于点F.若点F的坐标为(0,1),点D的坐标为(6,-1).
如图,在平面直角坐标系中,⊙P经过x轴上一点C,与y轴分别相交于A、B两点,连接AP并延长分别交⊙P、x轴于点D、点E,连接DC并延长交y轴于点F.若点F的坐标为(0,1),点D的坐标为(6,-1). 如图,抛物线y=ax2+bx+c(a≠0)的图象过点M(-2,
如图,抛物线y=ax2+bx+c(a≠0)的图象过点M(-2, 如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(-4,6),双曲线y=
如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(-4,6),双曲线y= 如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,OC=2,求阴影部分图形的面积(结果保留π).
如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,OC=2,求阴影部分图形的面积(结果保留π). 如图,彭园游乐场的摩天轮⊙P的最高处A到地面l的距离是23米,最低处B到地面l的距离是3米.从B处乘摩天轮绕一周需3分钟.小明从B处乘摩天轮一周的过程中,当他到地面l的距离恰好是18米的时候应为第
如图,彭园游乐场的摩天轮⊙P的最高处A到地面l的距离是23米,最低处B到地面l的距离是3米.从B处乘摩天轮绕一周需3分钟.小明从B处乘摩天轮一周的过程中,当他到地面l的距离恰好是18米的时候应为第