题目内容
10.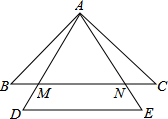 如图,在等腰△ABC中,AB=AC,△ADE是等边三角形,且DE∥BC,AD,AE分别交BC于点M,N.求证:BM=CN.
如图,在等腰△ABC中,AB=AC,△ADE是等边三角形,且DE∥BC,AD,AE分别交BC于点M,N.求证:BM=CN.
分析 利用等边三角形的性质和等腰三角形的性质,证明△ABM≌△ACN,利用全等三角形的对应边相等即可解答.
解答 解:∵△ADE是等边三角形,
∴∠D=∠E=60°,
∵DE∥BC,
∴∠AMN=∠D,∠ANM=∠E,
∴∠AMN=∠ANM=60°,
∴∠AMB=∠ANC=120°,
∵AB=AC,
∴∠B=∠C,
在△ABM和△ACN中,
$\left\{\begin{array}{l}{∠B=∠C}\\{∠AMB=∠ANC}\\{AB=AC}\end{array}\right.$
∴△ABM≌△ACN,
∴BM=CN.
点评 本题考查了全等三角形的性质定理与判定定理,解决本题的关键是证明△ABM≌△ACN.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
20.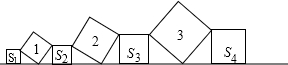 如图,直线l上依次摆放着一系列正方形,斜放置的正方形面积分别为1,2,3,…,n,正放置的正方形面积分别为S1,S2,S3,…,Sn,当n=100时,则S1+S2+S3+…+S100等于( )
如图,直线l上依次摆放着一系列正方形,斜放置的正方形面积分别为1,2,3,…,n,正放置的正方形面积分别为S1,S2,S3,…,Sn,当n=100时,则S1+S2+S3+…+S100等于( )
 如图,直线l上依次摆放着一系列正方形,斜放置的正方形面积分别为1,2,3,…,n,正放置的正方形面积分别为S1,S2,S3,…,Sn,当n=100时,则S1+S2+S3+…+S100等于( )
如图,直线l上依次摆放着一系列正方形,斜放置的正方形面积分别为1,2,3,…,n,正放置的正方形面积分别为S1,S2,S3,…,Sn,当n=100时,则S1+S2+S3+…+S100等于( )| A. | 2500 | B. | 2550 | C. | 2600 | D. | 2800 |
18. 如图所示,是六个棱长为1的立方块组成的一个几何体,其左视图的面积是( )
如图所示,是六个棱长为1的立方块组成的一个几何体,其左视图的面积是( )
 如图所示,是六个棱长为1的立方块组成的一个几何体,其左视图的面积是( )
如图所示,是六个棱长为1的立方块组成的一个几何体,其左视图的面积是( )| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
5.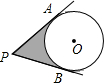 如图,从P点引⊙O的两切线PA、PA、PB,A、B为切点,已知⊙O的半径为3,∠P=60°,则图中阴影部分的面积为( )
如图,从P点引⊙O的两切线PA、PA、PB,A、B为切点,已知⊙O的半径为3,∠P=60°,则图中阴影部分的面积为( )
 如图,从P点引⊙O的两切线PA、PA、PB,A、B为切点,已知⊙O的半径为3,∠P=60°,则图中阴影部分的面积为( )
如图,从P点引⊙O的两切线PA、PA、PB,A、B为切点,已知⊙O的半径为3,∠P=60°,则图中阴影部分的面积为( )| A. | 9$\sqrt{3}$-3π | B. | 9$\sqrt{3}$-2π | C. | $\frac{9}{2}\sqrt{3}-3π$ | D. | $\frac{9}{2}\sqrt{3}-2π$ |
2.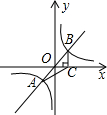 如图,过原点O的直线与双曲线y=$\frac{k}{x}$交于A、B两点,过点B作BC⊥x轴,垂足为C,连接AC,若S△ABC=5,则k的值是( )
如图,过原点O的直线与双曲线y=$\frac{k}{x}$交于A、B两点,过点B作BC⊥x轴,垂足为C,连接AC,若S△ABC=5,则k的值是( )
 如图,过原点O的直线与双曲线y=$\frac{k}{x}$交于A、B两点,过点B作BC⊥x轴,垂足为C,连接AC,若S△ABC=5,则k的值是( )
如图,过原点O的直线与双曲线y=$\frac{k}{x}$交于A、B两点,过点B作BC⊥x轴,垂足为C,连接AC,若S△ABC=5,则k的值是( )| A. | $\frac{5}{3}$ | B. | $\frac{5}{2}$ | C. | 5 | D. | 10 |
19.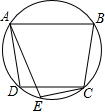 如图,在⊙O中,AB∥CD,∠BCD=100°,E为$\widehat{DC}$上的任意一点,A、B、C、D是⊙O上的四个点,则∠AEC的角度为( )
如图,在⊙O中,AB∥CD,∠BCD=100°,E为$\widehat{DC}$上的任意一点,A、B、C、D是⊙O上的四个点,则∠AEC的角度为( )
 如图,在⊙O中,AB∥CD,∠BCD=100°,E为$\widehat{DC}$上的任意一点,A、B、C、D是⊙O上的四个点,则∠AEC的角度为( )
如图,在⊙O中,AB∥CD,∠BCD=100°,E为$\widehat{DC}$上的任意一点,A、B、C、D是⊙O上的四个点,则∠AEC的角度为( )| A. | 110° | B. | 70° | C. | 80° | D. | 100° |
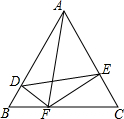 如图,△ABC是边长为a的等边三角形,DF⊥AB,EF⊥AC.
如图,△ABC是边长为a的等边三角形,DF⊥AB,EF⊥AC.
 如图,为了开发利用海洋资源,某勘测飞机测量一岛屿两端A、B的距离,飞机以距海平面垂直同一高度飞行,在点C处测得端点A的俯角为60°,然后沿着平行于AB的方向水平飞行了500米,在点D测得端点B的俯角为45°,已知岛屿两端A、B的距离541.91米,求飞机飞行的高度.(结果精确到1米,参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41)
如图,为了开发利用海洋资源,某勘测飞机测量一岛屿两端A、B的距离,飞机以距海平面垂直同一高度飞行,在点C处测得端点A的俯角为60°,然后沿着平行于AB的方向水平飞行了500米,在点D测得端点B的俯角为45°,已知岛屿两端A、B的距离541.91米,求飞机飞行的高度.(结果精确到1米,参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41)