题目内容
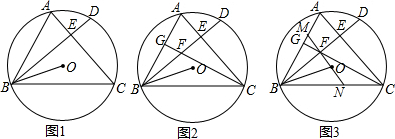
20. 如图,为了开发利用海洋资源,某勘测飞机测量一岛屿两端A、B的距离,飞机以距海平面垂直同一高度飞行,在点C处测得端点A的俯角为60°,然后沿着平行于AB的方向水平飞行了500米,在点D测得端点B的俯角为45°,已知岛屿两端A、B的距离541.91米,求飞机飞行的高度.(结果精确到1米,参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41)
如图,为了开发利用海洋资源,某勘测飞机测量一岛屿两端A、B的距离,飞机以距海平面垂直同一高度飞行,在点C处测得端点A的俯角为60°,然后沿着平行于AB的方向水平飞行了500米,在点D测得端点B的俯角为45°,已知岛屿两端A、B的距离541.91米,求飞机飞行的高度.(结果精确到1米,参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41)
分析 过点A作AE⊥CD于点E,过点B作BF⊥CD于点F,设高度为x米,在Rt△AEC中可得CE=$\frac{AE}{tan60°}$=$\frac{\sqrt{3}}{3}x$,在Rt△BFD中有DF=$\frac{BF}{tan45°}$=x,根据AB=EF=CD+DF-CE列出方程,解方程可求得x的值.
解答 解:过点A作AE⊥CD于点E,过点B作BF⊥CD于点F,
设高度为x米
∵AB∥CD,
∴∠AEF=∠EFB=∠ABF=90°,
∴四边形ABFE为矩形.
∴AB=EF,AE=BF.
由题意可知:AE=BF=x米,CD=500米.
在Rt△AEC中,∠C=60°,
∴CE=$\frac{AE}{tan60°}$=$\frac{\sqrt{3}}{3}x$(米).
在Rt△BFD中,∠BDF=45°,
∴DF=$\frac{BF}{tan45°}$=x(米).
∴AB=EF=CD+DF-CE,即500+x-$\frac{\sqrt{3}}{3}$x=541.91
解得:x=99
答:飞机行飞行的高度是99米.
点评 此题考查了俯角的定义、解直角三角形与矩形的性质.注意能借助俯角构造直角三角形并解直角三角形是解此题的关键,注意数形结合思想的应用.

练习册系列答案
相关题目
12.在平行四边形、菱形、矩形、正方形、等边三角形这五种图形中,既是轴对称图形,又是中心对称图形的有( )
| A. | 1种 | B. | 2种 | C. | 3种 | D. | 4种 |
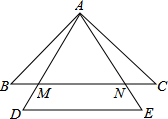 如图,在等腰△ABC中,AB=AC,△ADE是等边三角形,且DE∥BC,AD,AE分别交BC于点M,N.求证:BM=CN.
如图,在等腰△ABC中,AB=AC,△ADE是等边三角形,且DE∥BC,AD,AE分别交BC于点M,N.求证:BM=CN.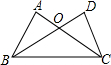 如图,△ABC和△DCB中,∠A=∠D=90°,边AC与DB相交于点O,要使△ABC≌△DCB,则需要添加的一个条件是AB=DC.(写出一种情况即可)
如图,△ABC和△DCB中,∠A=∠D=90°,边AC与DB相交于点O,要使△ABC≌△DCB,则需要添加的一个条件是AB=DC.(写出一种情况即可)