题目内容
15.方成同学看到一则材料,甲开汽车,乙骑自行车从M地出发沿一条公路匀速前往N地,设乙行驶的时间为t(h),甲乙两人之间的距离为y(km),y与t的函数关系如图1所示,方成思考后发现了图1的部分正确信息,乙先出发1h,甲出发20分钟后与乙相遇,…,请你帮助方成同学解决以下问题: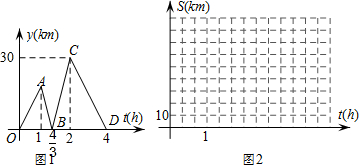
(1)分别求出线段BC,CD所在直线的函数表达式;
(2)当15<y<25时,求t的取值范围;
(3)分别求出甲、乙行驶的路程S甲、S乙与时间t的函数表达式,并在图2所给的直角坐标系中分别画出它们的图象.
分析 (1)设线段BC所在直线的函数表达式为y=k1t+b1,将点B、C的坐标代入其中得出关于k1、b1的二元一次方程组,解方程组即可求出结论;设线段CD所在直线的函数表达式为y=k2t+b2,将点C、D的坐标代入其中得出关于k2、b2的二元一次方程组,解方程组即可得出结论;
(2)根据线段CD可求出乙骑车的速度,从而得出线段OA的函数解析式,结合题意列出关于t的一元一次不等式,解不等式即可得出结论;
(3)根据图象求出甲开车的速度,由路程=速度×时间得出S甲、S乙与时间t的函数表达式,画出图形即可.
解答 解:(1)设线段BC所在直线的函数表达式为y=k1t+b1,
将点B($\frac{4}{3}$,0),点C(2,30)代入函数解析式,得
$\left\{\begin{array}{l}{\frac{4}{3}{k}_{1}+{b}_{1}=0}\\{2{k}_{1}+{b}_{1}=30}\end{array}\right.$,解得:$\left\{\begin{array}{l}{{k}_{1}=45}\\{{b}_{1}=-60}\end{array}\right.$.
故线段BC所在直线的函数表达式为y=45t-60($\frac{4}{3}$≤t≤2).
设线段CD所在直线的函数表达式为y=k2t+b2,
将点C(2,30),点D(4,0)代入函数解析式,得
$\left\{\begin{array}{l}{2{k}_{2}+{b}_{2}=30}\\{4{k}_{2}+{b}_{2}=0}\end{array}\right.$,解得:$\left\{\begin{array}{l}{{k}_{2}=-15}\\{{b}_{2}=60}\end{array}\right.$.
故线段CD所在直线的函数表达式为y=-15t+60(2<t≤4).
(2)乙骑车的速度为30÷(4-2)=15(km/h),
∴线段OA所在直线的函数表达式为y=15t(0≤t≤1),
∴点A的纵坐标为15.
当15<y<25时,即15<45t-60<25或15<-15t+60<25,
解得:$\frac{5}{3}$<t<$\frac{17}{9}$或$\frac{7}{3}$<t<3.
故当15<y<25时,t的取值范围为$\frac{5}{3}$<t<$\frac{17}{9}$或$\frac{7}{3}$<t<3.
(3)甲开车的速度15÷($\frac{4}{3}$-1)+15=60(km/h),
∴S甲=60(t-1)=60t-60(1≤t≤2),S乙=15t(0≤t≤4).
所画图形如图.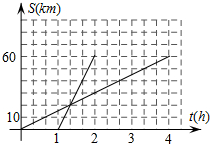
点评 本题考查了一次函数的应用、待定系数法求函数解析式以及一元一次不等式的应用,解题的关键是:(1)待定系数法求函数解析式;(2)列出关于时间t的一元一次不等式;(3)找出甲、乙的速度.本题属于中档题,难度不大,解决该题型题目时,结合图形解决问题是关键.

 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 △ABC在直角坐标系中的位置如图所示,若将△ABC绕点O旋转,点C的对应点为点D,其中A(1,2),B(-1,0),C(3,-1),D(-1,-3),则旋转后点A的对应点E的坐标为( )
△ABC在直角坐标系中的位置如图所示,若将△ABC绕点O旋转,点C的对应点为点D,其中A(1,2),B(-1,0),C(3,-1),D(-1,-3),则旋转后点A的对应点E的坐标为( )| A. | (-1,2) | B. | (0,-1) | C. | (1,-3) | D. | (2,-1) |
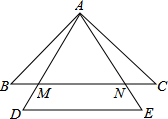 如图,在等腰△ABC中,AB=AC,△ADE是等边三角形,且DE∥BC,AD,AE分别交BC于点M,N.求证:BM=CN.
如图,在等腰△ABC中,AB=AC,△ADE是等边三角形,且DE∥BC,AD,AE分别交BC于点M,N.求证:BM=CN. 用圆规、直尺作图,不写作法,但要保留作图痕迹.
用圆规、直尺作图,不写作法,但要保留作图痕迹.