题目内容
20.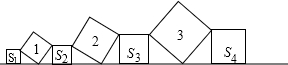 如图,直线l上依次摆放着一系列正方形,斜放置的正方形面积分别为1,2,3,…,n,正放置的正方形面积分别为S1,S2,S3,…,Sn,当n=100时,则S1+S2+S3+…+S100等于( )
如图,直线l上依次摆放着一系列正方形,斜放置的正方形面积分别为1,2,3,…,n,正放置的正方形面积分别为S1,S2,S3,…,Sn,当n=100时,则S1+S2+S3+…+S100等于( )| A. | 2500 | B. | 2550 | C. | 2600 | D. | 2800 |
分析 如图1,根据正方形的性质得AC=CD,∠ACD=90°,再根据等角的余角线段得∠BAC=∠DCE,则可根据“AAS”判定△ACB≌△DCE,得到AB=CE,BC=DE;由勾股定理得AC2=AB2+BC2=AB2+DE2,即Sb=Sa+Sc=5;如图2,由前面的结论可得S1+S2=1=1+2×0=1,S3+S4=3=1+2×1=3,S5+S6=1+2×2=5,…S99+S100=99,然后相加得到S1+S2+S3+…+S100=2500.
解答 解:如图1,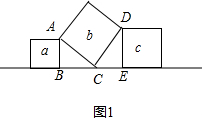 ∵a、b、c都是正方形,
∵a、b、c都是正方形,
∴AC=CD,∠ACD=90°,
∴∠ACB+∠DCE=90°,
而∠ACB+∠BAC=90°,
∴∠BAC=∠DCE,
在△ACB和△DCE中,
$\left\{\begin{array}{l}{∠ABC=∠CED}\\{∠BAC=∠DCE}\\{AC=CD}\end{array}\right.$,
∴△ACB≌△DCE(AAS),
∴AB=CE,BC=DE;
在Rt△ABC中,由勾股定理得:AC2=AB2+BC2=AB2+DE2,
即Sb=Sa+Sc=1+4=5;
如图2,由前面的结论可得S1+S2=1=1+2×0=1,
S3+S4=3=1+2×1=3,
S5+S6=1+2×2=5,
…
S99+S100=99,
∴S1+S2+S3+…+S100=1+3+5+…+99=2500.
故选:A.
点评 本题考查了全等三角形的判定与性质:全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.也考查了勾股定理和正方形的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.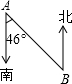 石家庄现在正在修建的地铁1号线大致是东西走向的,已知在白佛站往东有一个拐弯,现记弯道的两个端点分别为A,B,如图所示,若在A地测得地铁隧道的走向是南偏东46°,则为了使地铁隧道能够准确接通,在B地施工的地铁隧道的走向应为( )
石家庄现在正在修建的地铁1号线大致是东西走向的,已知在白佛站往东有一个拐弯,现记弯道的两个端点分别为A,B,如图所示,若在A地测得地铁隧道的走向是南偏东46°,则为了使地铁隧道能够准确接通,在B地施工的地铁隧道的走向应为( )
 石家庄现在正在修建的地铁1号线大致是东西走向的,已知在白佛站往东有一个拐弯,现记弯道的两个端点分别为A,B,如图所示,若在A地测得地铁隧道的走向是南偏东46°,则为了使地铁隧道能够准确接通,在B地施工的地铁隧道的走向应为( )
石家庄现在正在修建的地铁1号线大致是东西走向的,已知在白佛站往东有一个拐弯,现记弯道的两个端点分别为A,B,如图所示,若在A地测得地铁隧道的走向是南偏东46°,则为了使地铁隧道能够准确接通,在B地施工的地铁隧道的走向应为( )| A. | 北偏西46° | B. | 北偏西44° | C. | 南偏东46° | D. | 南偏西44° |
8.下列式子中与2ab2是同类项的是( )
| A. | 3ab | B. | 2b2 | C. | ab2 | D. | a2b |
12. 如图,满足下列条件中的哪一个,可得到AB∥CD( )
如图,满足下列条件中的哪一个,可得到AB∥CD( )
 如图,满足下列条件中的哪一个,可得到AB∥CD( )
如图,满足下列条件中的哪一个,可得到AB∥CD( )| A. | ∠1=∠2 | B. | ∠3=∠4 | C. | ∠1=∠4 | D. | ∠5=∠1+∠3 |
9.在同一直角坐标系中,函数y=$-\frac{2}{x}$与y=2x图象的交点个数为( )
| A. | 3 | B. | 1 | C. | 0 | D. | 2 |
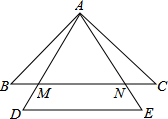 如图,在等腰△ABC中,AB=AC,△ADE是等边三角形,且DE∥BC,AD,AE分别交BC于点M,N.求证:BM=CN.
如图,在等腰△ABC中,AB=AC,△ADE是等边三角形,且DE∥BC,AD,AE分别交BC于点M,N.求证:BM=CN.