题目内容
6. 如图,已知矩形ABCD的四个顶点位于双曲线y=$\frac{k}{x}$上,且点A的横坐标为$\frac{\sqrt{5}-1}{2}$,S矩形ABCD=2$\sqrt{5}$,则k=1.
如图,已知矩形ABCD的四个顶点位于双曲线y=$\frac{k}{x}$上,且点A的横坐标为$\frac{\sqrt{5}-1}{2}$,S矩形ABCD=2$\sqrt{5}$,则k=1.
分析 先根据四边形ABCD是矩形,再根据两点间的距离公式用k表示出AB及BC的长,利用矩形的面积公式即可得出结论.
解答 解:∵矩形ABCD的四个顶点位于双曲线y=$\frac{k}{x}$上,
∴A与C,B与D关于原点对称,A与D,C与B关于直线x=y对称,
设A($\frac{\sqrt{5}-1}{2}$,$\frac{\sqrt{5}+1}{2}$k),则D($\frac{\sqrt{5}+1}{2}$k,$\frac{\sqrt{5}-1}{2}$),C(-$\frac{\sqrt{5}-1}{2}$,-$\frac{\sqrt{5}+1}{2}$k),B(-$\frac{\sqrt{5}+1}{2}$k,-$\frac{\sqrt{5}-1}{2}$),
∴AB=$\sqrt{(\frac{\sqrt{5}-1}{2}+\frac{\sqrt{5}+1}{2}k)^{2}+(\frac{\sqrt{5}+1}{2}k+\frac{\sqrt{5}-1}{2})^{2}}$=$\sqrt{-6+2\sqrt{5}+4k-(6-2\sqrt{5}){k}^{2}}$,AD=$\sqrt{(\frac{\sqrt{5}-1}{2}-\frac{\sqrt{5}+1}{2}k)^{2}+(\frac{\sqrt{5}+1}{2}k-\frac{\sqrt{5}-1}{2})^{2}}$=$\sqrt{-6+2\sqrt{5}+4k-(6-2\sqrt{5}){k}^{2}}$,
∵S四边形ABCD=AB•AD=2$\sqrt{5}$,
∴k=±1,
∵k>0,
∴k=1.
故答案为:1.
点评 本题考查了反比例函数系数k的几何意义,反比例函数的性质,反比例函数图象上点的坐标特点,矩形的性质,难度适中.

 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案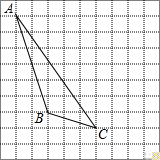 如图,在方格纸内将△ABC水平向右平移4个单位得到△A′B′C′.
如图,在方格纸内将△ABC水平向右平移4个单位得到△A′B′C′.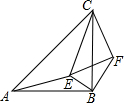 如图,△ABC和△CEF均为等腰直角三角形,E在△ABC内,∠CAE+∠CBE=90°,连接BF.
如图,△ABC和△CEF均为等腰直角三角形,E在△ABC内,∠CAE+∠CBE=90°,连接BF. 如图,将三角形纸片ABC沿DE折叠,使点A落在BC边上的点F处,且DE∥BC,当DE=2时,BC的长为( )
如图,将三角形纸片ABC沿DE折叠,使点A落在BC边上的点F处,且DE∥BC,当DE=2时,BC的长为( )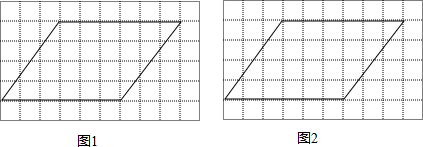
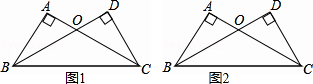
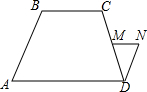 如图,在梯形ABCD中,AD∥BC,M是CD中点,MN∥AD,DN∥AB,设BC=a,AD=b(a<b),那么MN与a、b有怎样的数量关系.试加以证明.
如图,在梯形ABCD中,AD∥BC,M是CD中点,MN∥AD,DN∥AB,设BC=a,AD=b(a<b),那么MN与a、b有怎样的数量关系.试加以证明.