题目内容
1.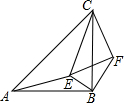 如图,△ABC和△CEF均为等腰直角三角形,E在△ABC内,∠CAE+∠CBE=90°,连接BF.
如图,△ABC和△CEF均为等腰直角三角形,E在△ABC内,∠CAE+∠CBE=90°,连接BF.(1)求证:△CAE∽△CBF.
(2)若BE=1,AE=2,求CE的长.
分析 (1)首先由△ABC和△CEF均为等腰直角三角形可得AC:BC=CE:CF,∠ACE=∠BCF;然后根据相似三角形判定的方法,推得△CAE∽△CBF即可;
(2)首先根据△CAE∽△CBF,判断出∠CAE=∠△CBF,再根据∠CAE+∠CBE=90°,判断出∠EBF=90°;然后在Rt△BEF中,根据勾股定理,求出EF的长度,再根据CE、EF的关系,求出CE的长是多少即可.
解答 (1)证明:∵△ABC和△CEF均为等腰直角三角形,
∴$\frac{AC}{BC}$=$\frac{CE}{CF}$=$\sqrt{2}$,
∴∠ACB=∠ECF=45°,
∴∠ACE=∠BCF,
∴△CAE∽△CBF;
(2)解:∵△CAE∽△CBF,
∴∠CAE=∠CBF,$\frac{AE}{BF}$=$\frac{AC}{BC}$=$\sqrt{2}$,
又∵$\frac{AE}{BF}$=$\frac{AC}{BC}$=$\sqrt{2}$,AE=2
∴$\frac{2}{BF}$=$\sqrt{2}$,∴BF=$\sqrt{2}$,
又∵∠CAE+∠CBE=90°,
∴∠CBF+∠CBE=90°,
∴∠EBF=90°,
∴EF2=BE2+BF2=12+($\sqrt{2}$)2=3,
∴EF=$\sqrt{3}$,
∵CE2=2EF2=6,
∴CE=$\sqrt{6}$.
点评 此题考查相似三角形的判定和性质,正方形的性质,掌握相似三角形的判定方法是解决问题的前提.

练习册系列答案
相关题目
11.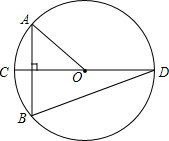 如图,⊙O的直径CD垂直于弦AB,∠AOC=40°,则∠CDB的度数为( )
如图,⊙O的直径CD垂直于弦AB,∠AOC=40°,则∠CDB的度数为( )
 如图,⊙O的直径CD垂直于弦AB,∠AOC=40°,则∠CDB的度数为( )
如图,⊙O的直径CD垂直于弦AB,∠AOC=40°,则∠CDB的度数为( )| A. | 40° | B. | 30° | C. | 20° | D. | 10° |
10. 如图,∠E+∠D=45°,则∠EFC的度数为( )
如图,∠E+∠D=45°,则∠EFC的度数为( )
 如图,∠E+∠D=45°,则∠EFC的度数为( )
如图,∠E+∠D=45°,则∠EFC的度数为( )| A. | 30° | B. | 60° | C. | 90° | D. | 45° |
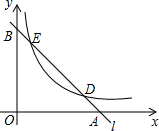 已知直线l分别与x轴、y轴交于A、B两点,与双曲线y=$\frac{m}{x}$(m≠0,x>0)分别交于D、E两点,若点D的坐标为(4,1),点E的坐标为(1,n)
已知直线l分别与x轴、y轴交于A、B两点,与双曲线y=$\frac{m}{x}$(m≠0,x>0)分别交于D、E两点,若点D的坐标为(4,1),点E的坐标为(1,n)
 如图,已知矩形ABCD的四个顶点位于双曲线y=$\frac{k}{x}$上,且点A的横坐标为$\frac{\sqrt{5}-1}{2}$,S矩形ABCD=2$\sqrt{5}$,则k=1.
如图,已知矩形ABCD的四个顶点位于双曲线y=$\frac{k}{x}$上,且点A的横坐标为$\frac{\sqrt{5}-1}{2}$,S矩形ABCD=2$\sqrt{5}$,则k=1.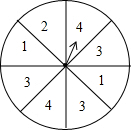 如图,一个可以自由转动的圆形转盘,转盘分成8个大小相同的扇形,上面分别标有数字1、2、3、4,指针的位置固定,转动的转盘停止后,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,当作指向右边的扇形).转动转盘一次,当转盘停止转动时,则指针指向标有“3”所在区域的概率为$\frac{3}{8}$.
如图,一个可以自由转动的圆形转盘,转盘分成8个大小相同的扇形,上面分别标有数字1、2、3、4,指针的位置固定,转动的转盘停止后,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,当作指向右边的扇形).转动转盘一次,当转盘停止转动时,则指针指向标有“3”所在区域的概率为$\frac{3}{8}$.