题目内容
17．先化简，再求值：（$\frac{4x+1}{2{x}^{2}+x}$+$\frac{4x}{2x+1}$）÷$\frac{1}{x}$，其中x=$\frac{\sqrt{2}-1}{2}$．分析 原式括号中两项通分并利用同分母分式的加法法则计算，同时利用除法法则变形，约分得到最简结果，把x的值代入计算即可求出值．
解答 解：原式=$\frac{4x+1+4{x}^{2}}{x（2x+1）}$•x=$\frac{（2x+1）^{2}}{x（2x+1）}$•x=2x+1，
当x=$\frac{\sqrt{2}-1}{2}$时，原式=$\sqrt{2}$．
点评 此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．
练习册系列答案
应用题作业本系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
8．
观察下面一组数：-1，2，-3，4，-5，6，-7，…．，将这组数排成如图的形式，按照如图规律排下去，则第11行中从左边数第10个数是（ ）
观察下面一组数：-1，2，-3，4，-5，6，-7，…．，将这组数排成如图的形式，按照如图规律排下去，则第11行中从左边数第10个数是（ ）| A． | -110 | B． | 110 | C． | -111 | D． | 111 |
如图，点A（1，4），B（-4，n）在双曲线y=$\frac{k}{x}$的图象上，直线AB分别交x轴、y轴于C，D，过点A作AE⊥x轴，垂足为E，过点B作BF⊥y轴，垂足为F，连接AF，BE交于点G．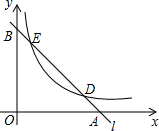
已知直线l分别与x轴、y轴交于A、B两点，与双曲线y=$\frac{m}{x}$（m≠0，x＞0）分别交于D、E两点，若点D的坐标为（4，1），点E的坐标为（1，n）
如图，已知矩形ABCD的四个顶点位于双曲线y=$\frac{k}{x}$上，且点A的横坐标为$\frac{\sqrt{5}-1}{2}$，S矩形ABCD=2$\sqrt{5}$，则k=1．