题目内容
11．
如图，将三角形纸片ABC沿DE折叠，使点A落在BC边上的点F处，且DE∥BC，当DE=2时，BC的长为（ ）| A． | 3 | B． | 4 | C． | 5 | D． | 6 |
分析 首先由DE∥BC与折叠的性质，可证得DE是△ABC的中位线，继而求得答案．
解答 解：∵DE∥BC，
∴∠ADE=∠B，∠EDF=∠BFD，
由折叠的性质可得：∠ADE=∠EDF，AD=DF，
∴∠B=∠BFD，
∴BD=DF，
∴AD=BD，
同理：AE=EC，
∴DE=$\frac{1}{2}$BC，
即BC=2DE=4．
故选B．
点评 此题考查了折叠的性质以及三角形中位线的性质．注意证得DE是△ABC的中位线是关键．
练习册系列答案
阅读快车系列答案
相关题目
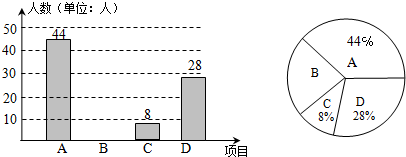
1．
为了解某校中学生获取资讯的主要渠道，该校随机抽取若干名学生进行调查，根据调查结果绘制条形统计图如图所示，其中A为电视、B为网格、C为报纸、D为身边的人、E为其他，茗茗想将图中用扇形统计图，则B所对应扇形圆心角的度数为（ ）
为了解某校中学生获取资讯的主要渠道，该校随机抽取若干名学生进行调查，根据调查结果绘制条形统计图如图所示，其中A为电视、B为网格、C为报纸、D为身边的人、E为其他，茗茗想将图中用扇形统计图，则B所对应扇形圆心角的度数为（ ）| A． | 130° | B． | 129.6° | C． | 128.6° | D． | 119.6° |
如图，点A（1，4），B（-4，n）在双曲线y=$\frac{k}{x}$的图象上，直线AB分别交x轴、y轴于C，D，过点A作AE⊥x轴，垂足为E，过点B作BF⊥y轴，垂足为F，连接AF，BE交于点G．
如图，在平面直角坐标系中，△ABC的三个顶点坐标为A（-3，4），B（-4，2），C（-2，1），△ABC绕原点逆时针旋转90°，得到△A1B1C1，△A1B1C1向右平移6个单位，再向上平移2个单位得到△A2B2C2．
如图，已知矩形ABCD的四个顶点位于双曲线y=$\frac{k}{x}$上，且点A的横坐标为$\frac{\sqrt{5}-1}{2}$，S矩形ABCD=2$\sqrt{5}$，则k=1．
16．
如图，小正方形的边长均为1，则∠1的正切值为（ ）
如图，小正方形的边长均为1，则∠1的正切值为（ ）| A． | $\frac{1}{5}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{2}$ |
