题目内容
5.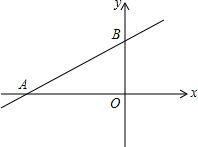 一次函数y=$\frac{\sqrt{3}}{3}$x+3的图象分别交x、y轴于A、B两点,是否在坐标轴上存在一点C使得△ABC为直角三角形?若有,请求出C点的坐标.
一次函数y=$\frac{\sqrt{3}}{3}$x+3的图象分别交x、y轴于A、B两点,是否在坐标轴上存在一点C使得△ABC为直角三角形?若有,请求出C点的坐标.
分析 求出直线与坐标轴的交点B、A的坐标,得出OA、OB的长度,分三种情况:①当∠ABC=90°时;②当∠ACB=90°时;③当∠BAC=90°时;分别由三角函数求出OC的长,即可得出C点的坐标.
解答 解:存在,理由如下:
一次函数y=$\frac{\sqrt{3}}{3}$x+3,
当x=0时,y=3;当y=0时,x=-3$\sqrt{3}$,
∴B(0,3),A(-3$\sqrt{3}$,0),
∴OA=3$\sqrt{3}$,OB=3,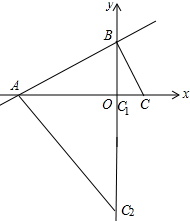
∴tan∠ABO=$\frac{OA}{OB}$=$\sqrt{3}$,
∴∠ABO=60°,
∴∠OAB=30°,
分三种情况:如图所示:
①当∠ABC=90°时,∠ACB=60°,
∴OC=$\frac{OB}{\sqrt{3}}$=$\frac{3}{\sqrt{3}}$=$\sqrt{3}$,
∴C($\sqrt{3}$,0);
②当∠ACB=90°时,C与O重合,
∴C(0,0);
③当∠BAC=90°时,∠ACO=60°,
∴OC=$\sqrt{3}$OA=3×3$\sqrt{3}$=9,
∴C(0,-9);
综上所述:存在一点C使得△ABC为直角三角形,C点的坐标为($\sqrt{3}$,0)或(0,0)或(0,-9).
点评 本题考查了一次函数图象上点的坐标特征、三角函数、坐标与图形性质;求出直线与坐标轴的交点B、A的坐标是解决问题的关键.

练习册系列答案
相关题目
20. 如图,直线m∥n,∠1=70°,∠2=30°,则∠A等于( )
如图,直线m∥n,∠1=70°,∠2=30°,则∠A等于( )
 如图,直线m∥n,∠1=70°,∠2=30°,则∠A等于( )
如图,直线m∥n,∠1=70°,∠2=30°,则∠A等于( )| A. | 30° | B. | 35° | C. | 40° | D. | 50° |
14.下列等式中,是一元一次方程的是( )
| A. | x2-3x+2=0 | B. | 3+1=4 | C. | 2x=0 | D. | x+y=1 |
 如图,菱形ABCD的对角线长分别为a、b.它的面积为S,以菱形ABCD各边中点为顶点作四边形A1B1C1D1,它的面积为S1,然后再以四边形A1B1C1D1的中点为顶点作四边形如此下去,得到四边形A2B2C2D2,它的面积为S2,如此下去,得到四边形AnBnCnDn,
如图,菱形ABCD的对角线长分别为a、b.它的面积为S,以菱形ABCD各边中点为顶点作四边形A1B1C1D1,它的面积为S1,然后再以四边形A1B1C1D1的中点为顶点作四边形如此下去,得到四边形A2B2C2D2,它的面积为S2,如此下去,得到四边形AnBnCnDn,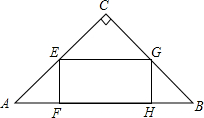 如图,矩形EFGH的顶点F,G在等腰Rt△ABC的斜边AB上,点E,H分别在直角边AC和BC上,EF=$\frac{1}{2}$EH,AB=6cm,求矩形EFGH的周长.
如图,矩形EFGH的顶点F,G在等腰Rt△ABC的斜边AB上,点E,H分别在直角边AC和BC上,EF=$\frac{1}{2}$EH,AB=6cm,求矩形EFGH的周长. 如图,已知直线AB∥DE.
如图,已知直线AB∥DE.