题目内容
9.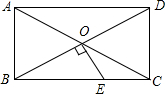 如图,?ABCD的对角线AC、BD交于点O,△AOB是等边三角形.
如图,?ABCD的对角线AC、BD交于点O,△AOB是等边三角形.(1)求证:四边形ABCD是矩形;
(2)若OE⊥BD交BC于E,求证:BE=2CE.
分析 (1)只要证明AC=BD即可解决问题.
(2)在RT△BOE中,易知BE=2EO,只要证明EO=EC即可
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AO=OC,BO=OD,
∵△ABO是等边三角形,
∴AO=BO=AB,
∴AO=OC=BO=OD,
∴AC=BD,
∴四边形ABCD是矩形.
(2)证明:∵四边形ABCD是矩形,
∴OB=OC,∠ABC=90°,
∵△ABO是等边三角形,
∴∠ABO=60°,
∴∠OBC=∠OCB=30°,∠BOC=120°,
∵BO⊥OE,
∴∠BOE=90°,∠EOC=30°,
∴∠EOC=∠ECO,
∴EO=EC,
∴BE=2EO=2CE.
点评 本题考查平行四边形的性质、矩形的判定、等边三角形的性质、等腰三角形的判定等知识,解题的关键是直角三角形30度角的性质的应用,属于中考常考题型.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
4.在实数1,-2,0,-0.5中,最小的实数是( )
| A. | 1 | B. | -2 | C. | 0 | D. | -0.5 |
14.下列等式中,是一元一次方程的是( )
| A. | x2-3x+2=0 | B. | 3+1=4 | C. | 2x=0 | D. | x+y=1 |
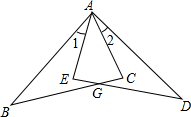 如图,在Rt△ACB和Rt△AED中,己知AB=AD,∠1=∠2,求证:EG=CG.
如图,在Rt△ACB和Rt△AED中,己知AB=AD,∠1=∠2,求证:EG=CG.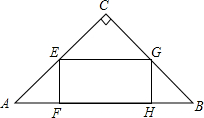 如图,矩形EFGH的顶点F,G在等腰Rt△ABC的斜边AB上,点E,H分别在直角边AC和BC上,EF=$\frac{1}{2}$EH,AB=6cm,求矩形EFGH的周长.
如图,矩形EFGH的顶点F,G在等腰Rt△ABC的斜边AB上,点E,H分别在直角边AC和BC上,EF=$\frac{1}{2}$EH,AB=6cm,求矩形EFGH的周长. 如图,四边形ABCD是边长为2的正方形,△CDE是等边三角形.
如图,四边形ABCD是边长为2的正方形,△CDE是等边三角形.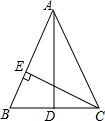 如图,在△ABC中,AB=AC=13,BC=10,D是BC的中点,CE⊥AB于E.
如图,在△ABC中,AB=AC=13,BC=10,D是BC的中点,CE⊥AB于E.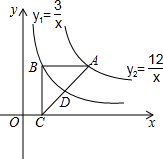 如图是反比例函数${y_1}=\frac{3}{x}$和${y_2}=\frac{12}{x}$在第一象限的图象,等腰直角△ABC的直角顶点B在y1上,顶点A在y2上,顶点C在x轴上,AB∥x轴,则CD:AD=$\frac{\sqrt{13}+1}{6}$.
如图是反比例函数${y_1}=\frac{3}{x}$和${y_2}=\frac{12}{x}$在第一象限的图象,等腰直角△ABC的直角顶点B在y1上,顶点A在y2上,顶点C在x轴上,AB∥x轴,则CD:AD=$\frac{\sqrt{13}+1}{6}$.