题目内容
2.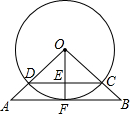 在△AOB中,AO=BO,以O圆心作圆和AB相切于点F,和OA,OB相交于点D,C,连接OF交于点E.
在△AOB中,AO=BO,以O圆心作圆和AB相切于点F,和OA,OB相交于点D,C,连接OF交于点E.(1)求证:CD∥AB;
(2)若2OE=3EF,求△AOB三边的比值;
(3)若CD=8,EF=2,求AB的长度.
分析 (1)根据三角形的内角和定理求出∠O,根据等腰三角形的性质求出∠OCD=∠ODC=30°,得出∠OCD=∠A即可;
(2)由已知条件得到OE:OC=3:5,根据切线性质得到OF⊥AB,通过△OCD∽△OAB,得到$\frac{OD}{CD}=\frac{OA}{AB}=\frac{5}{8}$,于是得到结论;
(3根据勾股定理得到OD=5,求得OE=3,根据相似三角形的想知道的$\frac{CD}{AB}=\frac{OE}{OF}$,于是得到结论.
解答 (1)证明:∵AO=BO,
∴∠A=$\frac{1}{2}$(180°-∠AOB),
∵OD=OC,
∴∠ODC=$\frac{1}{2}$(180°-∠AOB),
∴∠A=∠ODC,
∴CD∥AB;
(2)∵2OE=3EF,
∴OE:OF=3:5,
∴OE:OC=3:5,
∵圆和AB相切于点F,
∴OF⊥AB,
∴OF⊥CD
∴OD:DE=5:4,
∴OD:CD=5:8,
∵CD∥AB,
∴△OCD∽△OAB,
∴$\frac{OD}{CD}=\frac{OA}{AB}=\frac{5}{8}$,
∴△AOB三边的比值为:5:5:8;
(3)∵CD=8,EF=2,
∴DE=$\frac{1}{2}$CD=4,OE=OD-2,
∴OD2=OE2+DE2,
即OD2=(OD-2)2+42,
∴OD=5,
∴OE=3,
∵△OCD∽△OAB,
∴$\frac{CD}{AB}=\frac{OE}{OF}$,
∴AB=$\frac{40}{3}$.
点评 本题考查了切线的性质,相似三角形的判定和性质,平行线的判定,等腰三角形的性质,熟练掌握切线的性质定理是解题的关键.

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
14.下列能判定四边形是平行四边形的有( )
| A. | 一组对边相等,一组对角也相等 | |
| B. | 一组对边相等,一条对角线被另一条平分 | |
| C. | 一组对角相等,一条对角线被另一条平分 | |
| D. | 一组对角相等,过这组对角的顶点的对角线平分另一条对角线 |
 如图,在平面直角坐标系中,直线y=-4x+4与x轴、y轴分别交于A、B两点,以AB为边在第一象限内作正方形ABCD,顶点D在双曲线y=$\frac{k}{x}$上,将该正方形沿x轴负方向平移a个单位长度后,顶点C恰好落在双曲线y=$\frac{k}{x}$上,则a的值是( )
如图,在平面直角坐标系中,直线y=-4x+4与x轴、y轴分别交于A、B两点,以AB为边在第一象限内作正方形ABCD,顶点D在双曲线y=$\frac{k}{x}$上,将该正方形沿x轴负方向平移a个单位长度后,顶点C恰好落在双曲线y=$\frac{k}{x}$上,则a的值是( )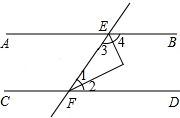 如图,直线AB,CD被EF所截,∠1=∠2,∠3=∠4,∠1+∠3=90°,那么AB与CD平行吗?为什么?
如图,直线AB,CD被EF所截,∠1=∠2,∠3=∠4,∠1+∠3=90°,那么AB与CD平行吗?为什么?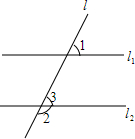 如图,若∠1+∠2=180°,则l1∥l2,试说明理由(填空).
如图,若∠1+∠2=180°,则l1∥l2,试说明理由(填空).