题目内容
12.如图①,在Rt△ABO中,∠A=90°,AB=2,AO=4,⊙O的半径为1,点C为BO的中点,点H为⊙O上一点,CH=2(1)求证;CH是⊙O的切线;
(2)如图②,过C作CD⊥CH交AO于D点,求tan∠ODC的值.
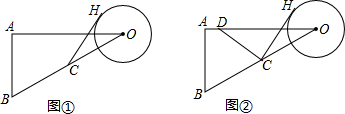
分析 (1)接OH,如图①,要证CH是⊙O的切线,只需证∠OHC=90°,只需运用勾股定理的逆定理就可解决问题;
(2)连接OH,设CH与OA交于点E,如图②,易证OH∥DC,则有∠ODC=∠HOE,要求tan∠ODC,只需求tan∠HOE,易证△CHO∽△OAB,则有∠HCO=∠AOB,即可得到EC=EO.设OE=x,则EC=x,EH=2-x,在Rt△EHO中运用勾股定理就可求出x,从而可求出EH,tan∠HOE.
解答 解:(1)连接OH,如图①,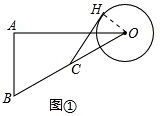
∵∠A=90°,AB=2,AO=4,
∴OB=$\sqrt{A{B}^{2}+O{A}^{2}}$=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$.
∵点C是OB的中点,
∴OC=$\frac{1}{2}$OB=$\sqrt{5}$.
∵CH=2,OH=1,
∴CH2+OH2=5=OC2,
∴∠OHC=90°,
∴CH与⊙O相切;
(2)连接OH,设CH与OA交于点E,如图②,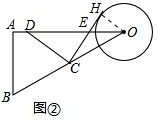
∵$\frac{OH}{AB}$=$\frac{CH}{OA}$=$\frac{OC}{OB}$=$\frac{1}{2}$,
∴△CHO∽△OAB,
∴∠HCO=∠AOB,
∴EC=EO.
设OE=x,则EC=x,EH=2-x.
在Rt△EHO中,
(2-x)2+12=x2,
解得x=$\frac{5}{4}$,
∴EH=2-$\frac{5}{4}$=$\frac{3}{4}$,
∴tan∠HOE=$\frac{EH}{OH}$=$\frac{3}{4}$.
∵CD⊥CH,
∴∠DCH=∠OHC=90°,
∴OH∥DC,
∴∠ODC=∠HOE,
∴tan∠ODC=tan∠HOE=$\frac{3}{4}$.
点评 本题主要考查了勾股定理及其逆定理、圆的切线的性质、等腰三角形的判定、三角函数、平行线的判定与性质、相似三角形的判定与性质等知识,证到EC=EO是解决第(2)小题的关键.

 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案| A. | -4 | B. | 4 | C. | 2 | D. | -2 |
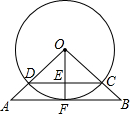 在△AOB中,AO=BO,以O圆心作圆和AB相切于点F,和OA,OB相交于点D,C,连接OF交于点E.
在△AOB中,AO=BO,以O圆心作圆和AB相切于点F,和OA,OB相交于点D,C,连接OF交于点E. 如图,∠A=75°,∠1=75°,∠3=105°
如图,∠A=75°,∠1=75°,∠3=105° 如图所示,P是直线AB外一点,CD与EF相交于P.若CD与AB平行,则EF与AB平行吗?为什么?
如图所示,P是直线AB外一点,CD与EF相交于P.若CD与AB平行,则EF与AB平行吗?为什么?