题目内容
6. 如图,在平面直角坐标系中,直线y=-4x+4与x轴、y轴分别交于A、B两点,以AB为边在第一象限内作正方形ABCD,顶点D在双曲线y=$\frac{k}{x}$上,将该正方形沿x轴负方向平移a个单位长度后,顶点C恰好落在双曲线y=$\frac{k}{x}$上,则a的值是( )
如图,在平面直角坐标系中,直线y=-4x+4与x轴、y轴分别交于A、B两点,以AB为边在第一象限内作正方形ABCD,顶点D在双曲线y=$\frac{k}{x}$上,将该正方形沿x轴负方向平移a个单位长度后,顶点C恰好落在双曲线y=$\frac{k}{x}$上,则a的值是( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 如图作CN⊥OB于N,DM⊥OA于M,CN与DM交于点F,CN交反比例函数于H,利用三角形全等,求出点C、点H坐标即可解决问题.
解答 解:如图作CN⊥OB于N,DM⊥OA于M,CN与DM交于点F,CN交反比例函数于H.
∵直线y=-4x+4与x轴、y轴分别交于A、B两点,
∴点B(0,4),点A(1,0),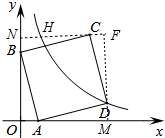
∵四边形ABCD是正方形,
∴AB=AD=DC=BC,∠BAD=90°,
∵∠BAO+∠ABO=90°,∠BAO+∠DAM=90°,
∴∠ABO=∠DAM,
在△ABO和△DAM中,
$\left\{\begin{array}{l}{∠BOA=∠AMD=90°}\\{∠ABO=∠DAM}\\{AB=AD}\end{array}\right.$,
∴△ABO≌△DAM,
∴AM=BO=4,DM=AO=1,
同理可以得到:CF=BN=AO=1,DF=CN=BO=4,
∴点F(5,5),C(4,1),D(5,1),k=5,
∴反比例函数为y=$\frac{5}{x}$
∴直线CN与反比例函数图象的交点H坐标为(1,5),
∴正方形沿x轴负方向平移a个单位长度后,顶点C恰好落在双曲线y=$\frac{k}{x}$上时,a=3,
故选A.
点评 本题考查反比例函数与一次函数的交点、正方形的性质、全等三角形的判定和性质等知识,解题的关键是添加辅助线构造全等三角形,属于中考常考题型.

练习册系列答案
相关题目
 解不等式5x+15>0,并将解集在数轴上表示出来.
解不等式5x+15>0,并将解集在数轴上表示出来.
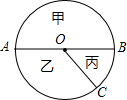 如图,AB是圆的直径,OC是圆的半径,扇形乙与扇形丙的面积比为2:1
如图,AB是圆的直径,OC是圆的半径,扇形乙与扇形丙的面积比为2:1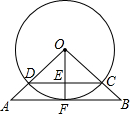 在△AOB中,AO=BO,以O圆心作圆和AB相切于点F,和OA,OB相交于点D,C,连接OF交于点E.
在△AOB中,AO=BO,以O圆心作圆和AB相切于点F,和OA,OB相交于点D,C,连接OF交于点E.