题目内容
11.解方程组:(1)$\left\{\begin{array}{l}{x+y=5}\\{x+z=12}\\{y=2z}\end{array}\right.$
(2)$\left\{\begin{array}{l}{x+y+z=26}\\{x-y=1}\\{2x+z-y=18}\end{array}\right.$.
分析 (1)把③代入①和②-④得出z=-7,再分别代入解答即可;
(2)先①-③和②+④得出y=9,再代入解答即可.
解答 解:(1)$\left\{\begin{array}{l}{x+y=5①}\\{x+z=12②}\\{y=2z③}\end{array}\right.$,
把③代入①得:x+2z=5④,
②-④得:z=-7,
把z=-7代入③得:y=-14,
把y=-14代入①得:x=19,
所以方程组的解是:$\left\{\begin{array}{l}{x=19}\\{y=-14}\\{z=-7}\end{array}\right.$,
(2)$\left\{\begin{array}{l}{x+y+z=26①}\\{x-y=1②}\\{2x+z-y=18③}\end{array}\right.$,
①-③得:-x+2y=8④,
②+④得:y=9,
把y=9代入②得:x=10,
把x=10,y=9代入①得:z=7,
所以方程组的解是:$\left\{\begin{array}{l}{x=10}\\{y=9}\\{z=7}\end{array}\right.$
点评 此题考查了解三元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
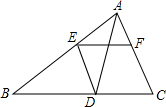 如图,AD是△ABC的角平分线,DE∥AC,EF∥BC,若AB=15,AF=4,则DE的长等于6.
如图,AD是△ABC的角平分线,DE∥AC,EF∥BC,若AB=15,AF=4,则DE的长等于6.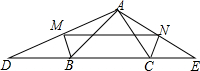 如图,BM、CN分别平分△ABC的外角∠ABD、∠ACE,过A分别作BM、CN的垂线,垂足分别为M、N,交CB、BC的延长线于D、E,连结MN.
如图,BM、CN分别平分△ABC的外角∠ABD、∠ACE,过A分别作BM、CN的垂线,垂足分别为M、N,交CB、BC的延长线于D、E,连结MN. 如图,已知AB=DC,AC=DB,AC与DB交于点M.过点C作CN∥BD,过点B作BN∥AC,CN与BN交于点N.
如图,已知AB=DC,AC=DB,AC与DB交于点M.过点C作CN∥BD,过点B作BN∥AC,CN与BN交于点N.