Question

3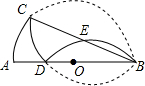．如图，AB是半圆O的直径，将半圆沿弦BC折叠，折叠后的圆弧与AB交于点D，再将弧BD沿AB对折后交弦BC于E，若E恰好是BC的中点，则BC：AB=$\frac{\sqrt{14}}{4}$．

Answer 1

分析 过D点作BC的垂线，垂足为M，延长DM交$\widehat{AB}$于D′，连接CD、DE、BD′，过点C作CF⊥AB于点F，由圆周角定理得出$\widehat{AC}=\widehat{CD′}=\widehat{CD}=\widehat{DE}$，得出AC=CD=DE，证出CM=EM，延长CM=$\frac{1}{4}$BC，证出DM∥AC，∴AD=$\frac{1}{4}$AB，设∠ABC=α，则∠ACF=α，得出AD=2AF，由三角函数得出AD=2AB•sin²α，因此$\frac{1}{4}$AB=2AB•sin²α，求出sinα=$\frac{\sqrt{2}}{4}$，由勾股定理和三角函数得出cosα=$\frac{BC}{AB}$=$\frac{\sqrt{14}}{4}$，即可得出结果．

解答 解：过D点作BC的垂线，垂足为M，延长DM交$\widehat{AB}$于D′，连接CD、DE、BD′，过点C作CF⊥AB于点F，如图所示：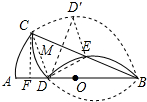
由等圆中圆周角相等所对的弧相等得：$\widehat{AC}=\widehat{CD′}=\widehat{CD}=\widehat{DE}$，
∴AC=CD=DE，
∴CM=EM，
∵E是BC的中点，
∴CM=$\frac{1}{4}$BC，
∵AB是半圆O的直径，
∴AC⊥BC，
∵DM⊥BC，
∴DM∥AC，
∴AD=$\frac{1}{4}$AB，
设∠ABC=α，则∠ACF=α，
∵AC=CD，
∴AD=2AF，
∵AF=AC•sinα，AC=AB•sinα，
∴AD=2AB•sin²α，
∴$\frac{1}{4}$AB=2AB•sin²α，
∴sinα=$\frac{\sqrt{2}}{4}$，即$\frac{AC}{AB}$=$\frac{\sqrt{2}}{4}$，
∴AB=2$\sqrt{2}$AC，BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{7}$AC，
∴cosα=$\frac{BC}{AB}$=$\frac{\sqrt{7}}{2\sqrt{2}}$=$\frac{\sqrt{14}}{4}$，
∴BC：AB=$\frac{\sqrt{14}}{4}$；
故答案为：$\frac{\sqrt{14}}{4}$．

点评 本题考查了翻折变换的性质、圆周角定理、勾股定理、三角函数等知识；熟练掌握圆周角定理，求出cosα是解决问题的关键．